David Lefebvre
Dans un long et passionnant article paru récemment sur le site du Café Pédagogique, Rémi Brissiaud développe un très intéressant argumentaire concernant l’enseignement de la division à l’école élémentaire à travers son histoire et les choix pédagogiques qui sous tendent cet enseignement. Ou plutôt ces enseignements, la variété des approches exposées en montrant fort bien la diversité. Son texte est à la fois très complet et très long, la version imprimée faisant entre vingt-cinq et trente pages ce qui n’est pas mince pour un article concernant les mathématiques, sujet qui a trop souvent tendance à faire fuir le public plutôt qu’à l’attirer. A tort certes, mais qu’y faire ? Continuer à expliquer sûrement, en gardant l’espoir que les arguments rationnels l’emportent sur la démagogie, souci que je partage entièrement avec l’auteur. Et justement, concernant lesdits arguments, j’aimerais bien revenir sur quelques points qui ont tendance à passer de moins en moins bien au fil des lectures que j’ai faites de ce texte.
Commençons par les points d’accord, ce sont les plus nombreux. Je souscris globalement à tout ce qui est dit sur l’enseignement de la division, partie la plus importante puisqu’elle représente assez exactement les deux tiers du texte. Je trouve ces réflexions à la fois pertinentes et salutaires et même si l’on peut toujours argumenter sur tel ou tel point de détail, je remercie Rémi Brissiaud d’avoir si clairement et si complètement exposé le problème. Je suis encore plus en accord avec l’auteur si c’est possible concernant l’enseignement des fractions, l’absence de « signification quotient » me paraissant poser gravement problème pour la suite à l’école élémentaire et encore plus au collège, moins toutefois que cet autre interdit encore plus stupide concernant les entiers relatifs. Qu’il ne soit pas question de travailler les procédures de calcul, bien sûr. Que les nombres inférieurs à zéro n’apparaissent à aucun moment dans les programmes étant par contre à mon sens une erreur.
Je suis par contre assez surpris par la charge finale contre l’intérêt des situations problèmes et plus particulièrement des problèmes de recherche, le point de vue développé étant basé sur un parallèle entre les programmes de 2002 en français et en mathématiques, point de vue qui m’apparaît pour le moins audacieux. Examinons les arguments avancés dans le paragraphe suivant :
De ce point de vue, les programmes de 2002 apparaissent très différents dans ce qu’ils préconisent pour l’apprentissage de l’écrit et pour celui des mathématiques. Concernant l’apprentissage de l’écrit, les programmes de 2002 ont officialisé une sorte de » recentrage » du discours pédagogique sur certaines conditions indispensables au progrès (la conceptualisation des relations grapho-phonologiques, la fréquentation d’œuvres littéraires, notamment). Concernant les mathématiques, en revanche, le discours sur les conditions indispensables à la conceptualisation de chacune des opérations arithmétiques perd de sa cohérence dans les programmes successifs et il tient de moins en moins de place au profit d’un discours plus général s’attachant essentiellement à décrire la démarche de pensée qu’il faudrait favoriser chez les élèves.
Il est surprenant pour le moins de parler de recentrage pour les programmes concernés en français. L’ouverture, vers la littérature justement, n’ayant jamais été aussi grande. Elle l’est même tellement que les classes de cycle 3 dans lesquels on lit dix ouvrages par an sont très courantes, au moins dans la circonscription et même dans le département, tous mes collègues en sont d’accord. Il est extrêmement rare d’entrer dans une classe du CE2 au CM2 dans laquelle les élèves seront amenés à lire seulement cinq ou six ouvrages dans l’année. Au prix et il faut être lucide quant à ce point, d’une réduction du temps passé à des exercices systématiques en orthographe, grammaire et conjugaison. D’une réduction des exercices systématiques, non des exigences dans ces domaines, les équipes et y compris les équipes de circonscription s’attachant à créer et diffuser des outils plus efficaces que, par exemple et sans vouloir vexer personne, le Bled ou assimilé. Je n’ai d’ailleurs jusqu’à présent guère vu de classe de collège ni même de lycée (du moins jusqu’en seconde) qui atteigne cette quantité de lecture. J’ajoute que l’enjeu n’est pas mince puisqu’il s’agit de permettre aux élèves, à tous les élèves justement, d’entrer dans la complexité de la langue écrite, point probablement plus déterminant pour la réussite dans le secondaire que les seules compétences dans le domaine de l’orthographe. Alors par pitié qu’on ne fasse pas sous prétexte de vouloir faire réussir tous et chacun de mauvais procès aux programmes actuels en mathématiques quand ils montrent, contrairement à ce qui est avancé dans le texte de Brissiaud, exactement le même souci et la même démarche en mathématiques, permettre l’entrée dans la complexité et dans la compréhension et non seulement l’acquisition de procédures qui seraient plus souvent fondées sur des automatismes qu’autre chose.
L’auteur le sait fort bien au demeurant, toutes les situations d’apprentissage proposées au fil de l’exposé étant des situations problèmes justement comme dans l’exemple suivant :
Ce jour-là, il est possible d’utiliser une situation d’anticipation comme la suivante : une collection de 163 cubes est formée (avec des cubes emboîtables, les élèves se répartissent le travail, ils forment 16 barres de 10 cubes et y ajoutent 3 cubes isolés, avant de mettre l’ensemble dans une boîte opaque). Le problème est posé : on va former des groupes de 25 avec ces 163 cubes. Combien peut-on former de groupes de 25 ? Restera-t-il des cubes isolés ?
C’est moi qui met en gras et si le problème est posé, justement, c’est qu’il y a une raison… Elle est simple : c’est comme ça qu’on apprend ! Dans un problème on peut se tromper. Et se tromper, il est important de le noter, de diverses façons. On peut aussi et c’est à la fois heureux et souhaitable arriver au résultat, en empruntant là aussi des voies différentes. Cet apprentissage, s’il est bien conduit, permet d’expliciter les différentes façons de procéder, seul moyen possible pour construire une connaissance partagée véritable. Avant d’aller plus loin dans cette voie qui est la thèse centrale de l’ouvrage que j’ai écrit en collaboration avec trois professeurs d’école, Eureka, des problèmes pour chercher, allons faire un tour par une très belle analogie dans le domaine du langage. Elle est décrite par un chercheur, Pierre Perruchet, dans un article, « Discordes autour de l’acquisition du langage », paru dans le numéro spécial de Les dossiers de La Recherche consacré à la mémoire, article disponible en ligne à : http://www.u-bourgogne.fr/LEAD/people/perruchet/pdf497Ko.pdf. La thèse de l’auteur est que l’élaboration de règles (dans le domaine du langage, nda) nécessite d’être exposé à des énoncés faux et présentés comme tels. Voici le début de l’article :
Lisez » savant aveugle » à haute voix. Une première fois sans faire la liaison. Une seconde fois en la faisant de façon prononcée. Comprenez-vous la même chose ? Non. Dans le premier cas, vous semblez parler d’un savant qui se trouve être aveugle ; dans le second cas, il s’agit d’un aveugle qualifié de savant .Votre compréhension se conforme là à une règle de la grammaire française qui ne souffre aucune exception, formulée ainsi dans la grammaire de Grevisse : » La liaison ne se fait jamais après la consonne finale d’un nom au singulier . «
Ce qui rend le phénomène étonnant, c’est que cette règle, pour aussi clairement formulée qu’elle soit, ne fait l’objet d’aucun enseignement. Vous ne l’avez jamais étudiée, vous seriez incapable de la verbaliser. Autrement dit, vous avez appris à la respecter, mais de façon implicite.
Il ne s’agit pas de transposer tel quel ce qui est écrit ici à l’enseignement des mathématiques, surtout que les développements qui font le corps de l’article complexifient considérablement le problème, néanmoins il serait déraisonnable de jeter en quelque sorte le bébé avec l’eau du bain. Et le bébé, j’ai bien peur que ce soit les situations problème. Situations qui donnent de la chair aux mathématiques lesquelles ne sauraient s’abstraire d’un fondement qui ne peut plus se réduire à l’utilitaire. Si j’ai besoin de faire des calculs j’ai une calculette… Donc soyons bien clairs sur un point, le calcul c’est comme la littérature, les sciences ou l’histoire géographie, ça ne sert à rien. Ou alors à comprendre le monde, ce qui ne se réduit pas à l’utilitaire mais ne permet aucunement de se dispenser de la signification.
Concernant ladite signification des problèmes pour les élèves, il serait possible de citer quelques réflexions de ceux qui ont participé à l’ouvrage, comme » Un problème c’est quand on a des ennuis. Ces problèmes là ce ne sont pas des ennuis, c’est un travail qui nous fait énormément réfléchir. Tous les élèves de notre classe adorent ça et on voudrait que tous les enfants de notre âge découvrent ça. » Ou alors » Maintenant on sait faire des problèmes. Avant on prenait tous les nombres de l’énoncé et on faisait des opérations. Maintenant, on réfléchit avant de faire les calculs. » Ou encore cette autre d’un enseignant : » Pour ça, moi je n’ai pas intérêt à manquer une seule séance de problèmes sinon je finis au pilori, les ailes étalées comme un cormoran qui sèche. » Mais enfin on ne peut pas se contenter de ces arguments, il va falloir en trouver de plus sérieux. Notons en passant qu’une activité que les élèves (et les maîtres) apprécient n’est pas forcément une activité à fuir à tout prix, réalité que notre école ferait bien de considérer avec un peu plus d’attention. Enfin, passons aux choses sérieuses.
Les objectifs tout d’abord, quels sont-ils ? On pourrait citer, par exemple : travailler en mathématiques comme dans le domaine des sciences : en formulant des hypothèses, en débattant, en confrontant des points de vue, en validant des productions. Ou bien mettre en oeuvre des séquences avec de vrais enjeux qui favorisent les échanges oraux entre élèves. Ou encore permettre des fonctionnements intellectuels jusqu’alors insoupçonnés dans la classe. Ou alors pour l’élève découvrir le côté » détective » des mathématiques et le plaisir du jeu, construire petit à petit un » cahier de recherche. » Ce qui impose quelques contraintes fortes, comme :
- Des situations problème ni évidentes ni impossibles.
- Que les élèves puissent jouer, simuler, se représenter la situation. Cette possibilité devant leur être proposée, voire montrée par l’enseignant.
- Qu’ils puissent proposer leur démarche pour en discuter et ce qu’ils aient ou non abouti au résultat. Ce qui entraîne l’acceptation des erreurs comme élément constitutif de l’apprentissage.
- Que toutes les démarches soient débattues afin que chacun puisse apprendre des autres. Ce qui implique un réel débat avec des questions posées par les élèves et non par l’enseignant.
- Qu’à l’issue de ce travail et après avoir été expliquées une ou plusieurs démarches soient validées
A ce stade il me semble important de faire remarquer que ce travail que nous avons conduit, nous l’avons conduit dans des classes accueillant une grande proportion d’élèves en difficulté, réalité attestée par les résultats observées aux évaluations CE2 et 6ème dans les écoles et les collèges du secteur. Et le souci constant, mené à bien au final, était de permettre à tous et à chacun non seulement de progresser mais aussi et surtout d’apprendre et de réussir. Il ne s’agit donc pas, comme il est écrit dans l’article, de laisser faire l’implicite dans une démarche finalement élitiste, bien au contraire. Considérons à titre d’exemple le problème suivant :
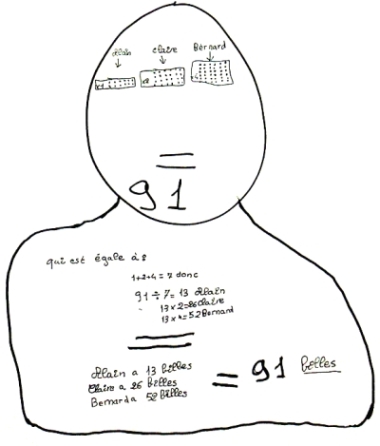
Alain a des billes, Claire en a deux fois plus et Bernard quatre fois plus. En tout ils en ont 91. Combien en ont-ils chacun ?
Voici trois productions d’élèves face à cette situation :
 |
 |
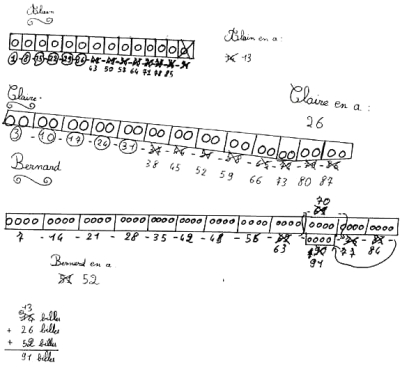 |
Sans rentrer dans le détail du travail, on voit facilement que les chemins suivis par les trois groupes considérés sont différents. Ce n’est pas non plus parce que trois groupes ont la même solution qu’elle est forcément exacte. Lors du débat qui suit la confrontation des productions, les élèves sont invités à vérifier ce résultat. Et comme la classe est maintenant face à une solution et trois démarches, doit-on toutes les retenir ou l’une d’elles semble-t-elle plus efficace et plus fiable ? Sans hésiter, les élèves choisissent la production « du bonhomme » (figure 1). C’est celle-ci qui sera retenue comme validation. J’insiste particulièrement sur la phase de débat, qui est organisé en mathématiques comme en littérature, à la différence qu’ici à la fin il s’agit aussi de prouver… Défendre un point de vue appuyé sur des arguments rationnels ne me parait pas de peu d’intérêt, surtout par les temps qui courent, et qui ont tendance à courir, comme le note justement Brissiaud, hors de toute rationalité. C’est pourquoi, si je partage sur beaucoup de points ses idées quant à l’enseignement des mathématiques, je pense qu’il nous faut tous être attentifs dans le débat à bien considérer tous les points de vue, fussent-ils au départ un peu éloignés de nos champs de pensée habituels. L’objectif est bien d’éviter les voies sans issue en développant nos arguments, non pas de fermer des portes en n’en gardant qu’une seule.
David Lefebvre
Inspecteur de l’éducation nationale
Dernier ouvrage publié :
Eurêka, des problèmes pour chercher – cycle 3 – éds MDI janvier 2006
Page publiée le 20-06-2006




