Dans cette dernière partie, Rémi Brissiaud invite à reconstruire une culture des premiers apprentissages numériques.

Les TICE au secours du basculement de 1986
La première possibilité serait de conserver l’hypothèse de Ermel (1990), celle qui est à la base de tous les programmes depuis 1986 : il faut, le plus tôt possible, enseigner le comptage « à la Gelman », celui qui s’effectue le plus souvent dans les familles, en théâtralisant la correspondance 1 mot – 1 objet. Cette hypothèse est conforme au cheminement ordinaire des enfants aux États-Unis, mais cela revient à gommer deux spécificités culturelles des enfants français : d’une part, ils disposent d’une langue qui, contrairement à l’anglais, explicite mal ce que sont les nombres et, d’autre part, ils ont la possibilité de fréquenter une école maternelle.
Les difficultés d’un tel cheminement vers la compréhension des nombres et l’accès au calcul, y compris aux États-Unis, sont bien documentées en psychologie. Cependant, des outils pédagogiques venant de ce pays peuvent améliorer ce cheminement ; ils prennent le plus souvent la forme de logiciels informatiques et il a été prouvé expérimentalement qu’ils améliorent les performances dans certaines tâches numériques, celles qui sont assez directement liées au comptage. Des outils élaborés en France dans le même esprit existent également. Les TICE vont-elles conduire à faire l’économie d’une critique du basculement de 1986 ?
La plupart de ces outils reposent sur un jeu de déplacement sur une file numérotée qui sert de piste et, donc, sur un enseignement du comptage numérotage. À ma connaissance, aucun progrès n’a été mis en évidence sur le long terme concernant le calcul exact. La façon remarquable dont les plus éminents pédagogues du 20e siècle décrivaient les conditions du progrès chez les élèves, le grand nombre de recherches en psychologie qui confortent leurs analyses et, enfin, l’étude de la DEPP conduisent à penser que le choix d’utiliser ce type d’outils en GS ou en CP, serait une erreur. Elle conduirait à retarder encore l’heure d’une authentique refondation de la pédagogie du nombre. Si l’on tient absolument à l’usage des TICE, faisons des appels à projet et encourageons les enseignants à utiliser des logiciels qui favorisent vraiment les apprentissages conceptuels des premiers nombres (comptage dénombrement, décompositions…).
Davantage de ludique et moins de symbolique
La deuxième possibilité sera débattue à partir de propos récents d’un des grands chercheurs actuels en psychologie, mais ces propos ont une portée qui va bien au-delà d’une prise de position personnelle. Ils semblent en effet apporter une réponse à un problème qui se pose effectivement : celui de la résurgence d’un phénomène de « primarisation de l’école maternelle ». Ces propos sont très relayés par le SNUIPP qui, depuis longtemps, alerte sur les dangers de ce phénomène. Les propos de ce chercheur doivent également être reçus très positivement par certains parents d’élèves dont les enfants souffrent de la primarisation de l’école maternelle. Ainsi, parmi les trois avenirs possibles, celui-ci n’est pas le plus improbable. Il a d’autant plus de chance d’être soutenu qu’un compromis avec la position qui vient d’être exposée n’est pas si difficile que cela à trouver, l’usage de logiciels enseignant le comptage numérotage en GS étant compatible avec cette deuxième possibilité.
Il y a deux questions auxquelles le chercheur qui s’est fait le porte parole de cette deuxième possibilité, apporte des réponses différentes de celles avancées dans ce texte : comment, en PS et en MS, faut-il enseigner les 3 – 4 premiers nombres et faut-il, en GS, continuer à enseigner le comptage « à la Gelman » ? Elles vont être successivement abordées.
Comment, en PS et en MS, faut-il enseigner les 3 – 4 premiers nombres ?
Dans le numéro d’avril 2012 de « Fenêtres sur cours », le journal du SNUIPP, la question suivante est posée à ce chercheur : « Quelles activités peut-on proposer à l’école maternelle pour aider les enfants dans leurs premiers apprentissages ? » et il répond : « C’est une question importante. Faut-il mettre en place très tôt des exercices avec l’objectif de procéder à un enseignement de l’arithmétique ? ou bien plutôt proposer des activités à dominante ludique avec l’idée d’aborder la manipulation des quantités, l’ajout, le retrait sans l’évoquer en termes symboliques ? La tentation pour les adultes de vouloir que les enfants utilisent et manipulent les noms des nombres entre deux ans et demi et quatre ans va à l’encontre des recherches qui montrent que l’enfant a besoin de beaucoup de temps pour construire de façon durable et articulée les nombres de 1 à 5. »
Il faut commencer par souligner les aspects positifs d’une telle prise de position : oui, comme Viviane Bouysse l’a récemment rappelé, l’école maternelle s’est primarisée au sens où des activités qui étaient auparavant l’apanage de l’école élémentaire se sont diffusées à l’ensemble de l’école primaire, parfois pour le meilleur, souvent pour le pire. L’une des conséquences est évidemment que les activités ludiques sont en régression à l’école maternelle. Par ailleurs, il est vrai que les recherches en psychologie ont montré que l’enfant a besoin de beaucoup de temps pour construire de façon articulée les nombres de 1 à 5. On pourrait même ajouter que les 5 premiers nombres se construisent dans l’ordre : on ne peut pas espérer qu’un enfant comprenne le nombre 3 s’il ne comprend pas les nombres 1 et 2 ; on ne peut pas espérer qu’un enfant comprenne le nombre 4 s’il ne comprend pas les nombres 1, 2 et 3 ; on ne peut pas espérer…
Mais, parce qu’il y a un « mais », on comprend mal ce que veut dire « aborder la manipulation des quantités, l’ajout, le retrait sans l’évoquer en termes symboliques » : cela veut-il dire sans parler ? De façon plus nette, il faut absolument l’affirmer : ce chercheur ne devrait pas reprocher aux adultes « de vouloir que les enfants utilisent et manipulent les noms des nombres entre deux ans et demi et quatre ans ». En effet, ces adultes ont raison de procéder ainsi s’il s’agit des 3 premiers nombres et si les noms de nombres sont utilisés pour exprimer les décompositions de ces petits nombres. Des milliers d’enseignants le font dès la PS et aucune recherche ne prouve que cela nuirait.
Il s’agit d’une interview et il se pourrait que les propos attribués à ce chercheur reflètent mal ce qu’il pense. Cependant, le compte-rendu de son intervention à l’Université d’Automne 2012 du SNUIPP affirme : « Un enfant ne comprend pas spontanément qu’une carte de « deux lions » va avec une carte de « deux fourmis »… Il faut bien attendre quatre ans pour que cela soit acquis… » Le journaliste qui signe ce compte rendu choisit d’ailleurs comme titre une formule qui résonne comme un mot d’ordre : « N’allez pas trop vite ». Ce mot d’ordre sera compris par de nombreux enseignant comme : « Ne vous y prenez pas trop tôt ». Il aurait été préférable de dire : « Enseignez les premiers nombres dès que l’enfant entre dans le langage, mais enseignez -les bien ».
Certes, un enfant ne comprend pas spontanément le nombre 2 parce qu’il doit apprendre à distinguer les actions permettant de former les collections de 2 unités des actions qui conduisent à des collections plus nombreuses. Mais il est possible de lui enseigner le nombre 2 à l’école dès qu’il entre dans le langage. Si l’enseignant renonce à tout usage du mot « deux » en tant que numéro ; s’il commente à haute voix ses propres actions lorsque lui-même forme une collection de 2 chaises, de 2 enfants… : « J’ai besoin de deux chaises, j’en prends une et encore une ; ça y est, j’ai deux chaises » ; s’il demande régulièrement à cet enfant de lui donner deux cubes, en reformulant cette demande : « un cube et encore un autre », s’il effectue ce type de demande en variant les unités, il n’y aucune raison pour qu’il faille attendre quatre ans pour que l’enfant comprenne le nombre 2 et même le nombre 3.
Ce point de désaccord est crucial. En effet, lorsqu’on enseigne les 3 premiers nombres précocement en explicitant leurs décompositions, cela conditionne toute la suite des apprentissages numériques, notamment pour les enfants qui ne bénéficient pas d’échanges familiaux dans lesquels les mots-nombres ont une signification cardinale. C’est vraisemblablement à cet âge que l’école peut influer de la manière la plus efficace pour un accès plus démocratique à de bonnes connaissances numériques.
Tous les parents lecteurs de ce texte, savent que leurs enfants, à 4 ans, ont souvent compris les 4 premiers nombres. Ils n’ont généralement pas pleinement conscience de ce qui a été crucial dans ce progrès : de nombreux échanges langagiers où les mots-nombres de « un » à « quatre » ont été utilisés avec leur signification cardinale (« les deux yeux », « les trois ours » par exemple). N’est-ce pas la première des responsabilités des enseignants de PS et de MS que de permettre à l’ensemble des enfants de bénéficier de tels échanges ? On sait que les enfants issus de milieux socioculturels éloignés de cette problématique pédagogique, réussissent beaucoup moins bien que les autres. N’est-ce pas la première des responsabilités des enseignants de PS et de MS que de permettre à ces enfants-là de bénéficier d’échanges encore plus explicites que ceux que l’on observe habituellement dans les familles parce qu’ils facilitent l’interprétation des actions d’ajout et de retrait ? L’enjeu de ce premier point de désaccord est donc la démocratisation de l’enseignement des nombres.
Faut-il, en GS et au CP, enseigner le comptage numérotage (« à la Gelman ») ?
On lit dans le compte-rendu de l’intervention du même chercheur à l’Université d’Automne du SNUIPP que l’enfant doit : « dire les noms des nombres sans oubli ni erreur d’ordre, en vérifiant le principe de correspondance terme-à-terme entre nom et objet, par pointage successif canonique : après avoir dénombré, l’enfant doit savoir dire « combien il y en a en tout, sans recompter ». Si on joue avec les enfants avec une « marionnette qui ne sait pas compter », à qui il faut apprendre à compter, on peut multiplier les situations d’erreurs (oubli d’un numéro…) jusqu’à ce que chacun sache ce qu’il faut faire pour réussir. »
Revoilà donc l’entraînement au respect des principes du comptage selon Gelman ! Il est scientifiquement prouvé aujourd’hui qu’une large fraction d’enfants (1/3 dans l’étude citée précédemment de Sarnecka et Carey) répètent le dernier mot d’un comptage numérotage alors que ce comptage est un comptage mécanique. Pourquoi faudrait-il les entraîner à utiliser une « règle du dernier mot prononcé » ? D’après la logique de l’exposé, l’activité décrite doit se situer vers la GS, ce qui est un peu moins pernicieux qu’en petite section. Mais encore une fois, c’est ce type d’enseignement qui, entre 1923 et 1986, a été fortement critiqué et même rejeté dans la culture pédagogique française. Que ce soit en GS, que ce soit au début du CP, il y a toujours quelques enfants qui n’ont pas encore compris les premiers nombres et ce type d’entraînement a pour eux des effets délétères.
Même pour les autres élèves, il n’est pas à recommander. Pendant des dizaines d’années, les écoliers français se sont passé de ce type d’entraînement qui fait obstacle au calcul et, de fait, ils calculaient mieux. L’étude de la DEPP conduit à conclure que mieux vaut ne rien faire que ce type d’entraînement. Et, d’un point de vue théorique, on comprend bien pourquoi il en est ainsi : le comptage numérotage privilégie une autre signification des mots utilisés que celle des nombres cardinaux et du calcul et il oblige à un apprentissage implicite de ce dernier (sauf à répéter les « tables » par cœur).
Dans l’école française d’aujourd’hui, quand la théorie de Gelman sort par la porte (abandon de l’idée que les enfants comprendraient les principes de manière précoce, grâce à une connaissance innée), elle rentre par la fenêtre (entraînement à compter en respectant ces principes en GS et/ou au CP). C’est certainement une conséquence du fait que l’enseignement du comptage « à la Gelman » est aussi celui de sens commun. Pourtant, aucun spécialiste n’a encore argumenté afin que l’on comprenne pourquoi il faudrait choisir d’enseigner le comptage sous la forme du comptage numérotage plutôt que sous celle du comptage dénombrement. Pourquoi faudrait-il nécessairement qu’à l’école, les enfants apprennent le comptage comme cela se fait le plus souvent dans les familles ?
De nombreux arguments contre un tel enseignement ont été avancés dans ce texte. En voici un autre. Auparavant, il faut rappeler que dans cette activité, la poupée se trompe parfois parce qu’elle saute un mot-nombre lors de son comptage numérotage. Elle compte ainsi, par exemple : « 1 (un objet est pointé) ; 2 (un autre objet est pointé) ; 3 (un autre) ; 4 (un autre) ; 6 (le dernier objet est pointé) ; il y a six jetons ». Pour les défenseurs de cette activité, c’est un moyen d’enseigner le « principe de suite stable » (il faut dire les mots- nombres dans l’ordre, sans en oublier). Imaginons que la poupée fasse la même erreur, mais dans le contexte d’un comptage dénombrement explicite. La poupée déplacerait successivement les 5 cubes d’une collection, par exemple, en disant : « 1 ; et encore 1, 2 ; et encore 1, 3 ; et encore 1, 4 ; et encore 1, 6 ; il y a 6 jetons » ; et la tâche des enfants serait, comme dans l’activité originelle, de trouver l’erreur. Lorsqu’on échange avec des enseignants chevronnés à propos d’un tel scénario d’activité, ils sont dubitatifs. Cela ne leur plait guère de mettre en scène l’erreur qui consiste à dire à un enfant que 4 plus 1 est égal à 6 pour qu’il proteste en disant que c’est faux. Interrogeons-nous : pourquoi la mise en scène d’erreurs ne soulève-t- elle aucune objection dans un cas alors qu’elle indispose dans l’autre ? Ne serait-ce pas parce que, dans un cas, il s’agit d’un apprentissage qui peut se réaliser sans signification alors que dans l’autre, on vise la compréhension ?
Il y a de toute évidence des confusions à lever : l’activité de la marionnette qui se trompe est une façon très ludique d’apprendre à respecter les règles du comptage « à la Gelman ». Mais pour de nombreux élèves, cela les met dans une situation similaire à celle du jeu « Jacques a dit… » : ils sont conduits à respecter des règles qui n’ont aucun raison sinon le bon vouloir de l’adulte qui anime le jeu. On peut apprendre mal de façon ludique. A l’école, il faut rechercher des activités ludiques qui permettent de bien apprendre.
Ceux qui, aujourd’hui, mettent en avant les dysfonctionnements résultant de la primarisation de l’école maternelle, qui appellent à plus de manipulation, à plus de jeu, ont raison. Mais si cela ne s’accompagne pas d’une critique du basculement de 1986, l’Ecole de la République sera perdante sur tous les tableaux : celui de la démocratisation de l’enseignement des nombres, celui de l’élévation générale du niveau en calcul des écoliers français et, en fin de compte, celui de l’autonomie de l’école face aux lubies de tels ou tels personnalités ou mouvements politiques. Immanquablement, en effet, il y aura dans le futur un autre ministre qui appellera alors à moins de jeu et à plus de symbolique afin que les élèves « se remettent au travail ». À moins qu’il demande carrément d’en finir avec l’école maternelle française…
Poser le problème ainsi, ce serait fermer la porte, peut-être de façon définitive, à la possibilité d’une véritable culture professionnelle chez les enseignants de l’École de la République, ce serait permettre que des questions qui sont avant tout pédagogiques restent aisément instrumentalisées dans un sens où dans l’autre par des responsables politiques pour des opérations de communication.
Reconstruire une culture pédagogique des premiers apprentissages numériques
En effet, la troisième et dernière possibilité consiste à s’engager dans la reconstitution d’une culture professionnelle qui intègre les leçons du passé. Il faut former les enseignants à l’histoire des discours et des pratiques scolaires : que disaient les enseignants qui nous ont précédés ? Que leur demandait-on de faire dans leur classe ? Quels outils utilisaient-ils ? Sur quelles connaissances en psychologie les prescripteurs fondaient-ils leurs convictions ? Sur quels critères décidait-on que telle ou telle pratique pédagogique « marche », etc.
Il faut que cette culture professionnelle enveloppe la dimension langagière des principaux apprentissages scolaires (les mots-nombres sont des noms et des adjectifs qui font partie de la langue). On dispose en effet de théories générales très performantes sur la façon dont un enfant qui entre dans le langage s’approprie le lexique. Il faut s’interroger sur ce que nous disent ces théories dans le cas particulier où ces mots sont des mots-nombres. La théorie d’Ellen Markman (1979, 1980), par exemple, permet de comprendre pourquoi les enfants interprètent les mots-nombres comme des sortes de numéros lors d’un comptage « à la Gelman ». Et, quand on utilise des travaux de psychologie, il faut savoir s’ils ont été menés avec des enfants anglophones ou francophones. On a vu que ce n’est pas anodin. Il faut également former les enseignants à reconnaître les difficultés résultant de la polysémie du mot « un » dans notre langue, etc.
Insistons : il s’agit de reconstruire une culture professionnelle qui intègre les leçons du passé et qui, si possible, aille au-delà de ce qu’était la culture professionnelle d’antan. Ainsi, un certain nombre de distinctions avancées ces 25 dernières années, semblent indispensables aujourd’hui parce qu’elles permettent de comprendre pourquoi les pédagogues ont, dans l’histoire, apprécié alternativement en termes de rejet et d’engouement certains outils culturels comme le comptage, l’usage des configurations numériques (les points du dé, les doigts, par exemple) ou encore celui des doigts pour trouver le résultat d’un ajout ou d’un retrait. Chacun de ces outils culturels a été tantôt interdit, tantôt prôné, chacun d’eux a été l’objet de débats passionnés qui conduisaient à des positions partisanes.
La première de ces distinctions indispensables est, bien entendu, celle entre comptage numérotage et comptage dénombrement : on aura compris que, selon que l’on enseigne l’une ou l’autre de ces deux formes de comptage, l’effet pédagogique est très différent et que bien des malentendus pourraient être levés grâce à cette distinction. Il existe un critère opérationnel simple pour procéder à cette distinction : quelle est la correspondance terme à terme privilégiée ?
Une autre distinction concerne les configurations numériques : les points du dé, les traits que l’on dessine les soirs d’élection en formant un carré avec une diagonale pour figurer 5 et, bien entendu, les doigts. Dans l’expression « configuration numérique », le mot « configuration » renvoie à l’idée de figure ou d’image alors que « numérique » renvoie à celle de nombre. Ces deux idées fonctionnent simultanément chez l’adulte : les soirs d’élection, face à la figure du carré et de sa diagonale, on « voit » le nombre 5. Il n’en est rien chez de nombreux enfants de maternelle. Il y a longtemps déjà, Piaget nous a alerté : la figure (ou l’image) peut faire obstacle au nombre. L’enfant exprimant qu’il a 3 ans en montrant le pouce, l’index et le majeur, très souvent, n’a souvent aucune idée qu’il montre ainsi le nombre 3 parce qu’il ne montre pas : « un, un et encore un », il montre : son pouce, son index et son majeur. L’adulte montrerait-il 3 avec l’index, le majeur et l’annulaire à cet enfant, que celui-ci ne reconnaîtrait plus ce qu’il associe au mot « trois » parce que l’image en a changé. En fait, lorsque l’enfant montre le pouce, l’index et le majeur, il ne considère pas ces doigts comme dépourvus de leur qualité afin de former chacun une unité : il n’y a pas de nombre. Pour bien identifier les cas où les configurations sont d’authentiques symboles numériques, j’ai proposé d’appeler celles-ci des collections-témoins (de points, de traits, de doigts…).
Cette distinction entre les configurations (non numériques) et les collections-témoins est tout aussi essentielle que celle entre le comptage numérotage et le comptage dénombrement. De même qu’il existe un critère simple pour distinguer comptage numérotage et comptage dénombrement, il en existe un pour distinguer une configuration non numérique et une collection-témoin : la substituabilité des éléments utilisés pour former la collection. Lorsqu’un enfant montre 3 doigts dont le pouce, on est certain qu’il utilise une collection-témoin de doigts et non une configuration non numérique seulement s’il sait que le pouce vaut « un » comme l’annulaire et, donc, s’il sait qu’il peut substituer ce dernier au premier. La distinction entre configuration et collection-témoin est fondamentale parce que jamais une configuration, lorsqu’elle est une image, ne provoque la sorte d’ « illumination » conduisant à considérer 4 comme 2 + 2 ou comme 3 + 1 ; « illumination » que Piaget, avec raison, préférait interpréter comme une réflexion sur des actions.
Enfin, dernière distinction : celle entre le comptage sur les doigts et le calcul sur les doigts. Pour définir ce dernier, considérons l’exemple d’un enfant de 4 ans ; 6 mois qui cherche 6 différences entre deux dessins qui, à première vue, sont ceux d’un même paysage (Brissiaud, 1991). Or, en dépit des apparences, ces deux dessins diffèrent par 6 détails (il s’agit donc de trouver « 6 erreurs » dans la copie du dessin). Ce jeu lui a été proposé parce qu’il maîtrise bien l’utilisation de collections-témoins de doigts jusqu’à 6. Il sait donc représenter 6 de la manière qui est canonique en France : une main complète plus le pouce de l’autre main, les deux pouces étant l’un à côté de l’autre. Alors que l’enfant a déjà trouvé 4 erreurs et qu’il les a entourées, l’adulte lui demande combien il doit encore en trouver et il répond « deux » en montrant les deux pouces.
Le schéma ci-dessous permet de comprendre son raisonnement : dans la collection-témoin canonique de 6, cet enfant a isolé 4 doigts parmi les 5 (ce sont les 4 erreurs de copie qu’il a déjà repérées) et il montre les 2 doigts restants (ce sont les erreurs qu’il faut encore chercher).
Il ne s’agit évidemment pas d’un comptage sur les doigts, encore moins de la « gesticulation digitale » qu’évoquait Henri Canac. Dans le comptage sur les doigts, ceux-ci sont égrenés les uns après les autres alors que le calcul sur les doigts correspond à l’usage de stratégies de décomposition-recomposition. On remarquera qu’un enfant ne peut calculer sur ses doigts que s’il utilise la propriété de substituabilité des doigts évoquée précédemment (ici, les collections-témoins que cet enfant utilise pour 4 et pour 2 ne sont pas les collections canoniques). Seul l’usage de collections-témoins permet l’accès au calcul, l’usage de configurations non numériques l’interdit. Toutes les études montrent que les enfants « mal débutés » s’enferment dans le comptage 1 à 1 sur les doigts alors que tous les exemples documentés d’enfants qui calculent sur leurs doigts (enfants asiatiques, monographie d’enfant français qui calcule sur ses doigts dès 4 ans, certains enfants sourds-profonds…) les décrivent comme progressant rapidement (Fuson & Kwon, 1991 ; Brissiaud, 1995b).
Il faut insister sur le fait que toutes ces distinctions, comptage numérotage et comptage dénombrement, configurations et collections-témoins, comptage sur les doigts et calcul sur les doigts, doivent nécessairement faire partie de la culture professionnelle d’un enseignant de maternelle. En effet, chacune permet de différencier deux comportements qu’une personne non informée ne peut pas distinguer. Celle-ci voit seulement un enfant qui compte, un enfant qui regarde des points, un enfant qui utilise ses doigts pour résoudre un problème. Or, l’un de ces comportements est compatible avec un parcours d’échec alors que l’autre est typique d’un parcours de réussite. Accepterait-on qu’un médecin ne sache pas, en regardant des grains de beauté sur la peau de ses patients, distinguer ceux qui sont sans danger et ceux qui pourraient l’alarmer ? Comment un futur document institutionnel accompagnant l’actuelle refondation de la pédagogie des premiers apprentissages numériques à l’école pourrait-il faire fi de distinctions fondamentales pour les pratiques enseignantes ?
Une chance historique à ne pas rater
Il y a donc bien besoin de débattre. L’enjeu est la reconstruction d’une culture professionnelle qui tisse des liens entre l’histoire des discours et des pratiques pédagogiques, les connaissances actuelles sur la façon dont les enfants de maternelle apprennent à calculer et les techniques professionnelles d’aujourd’hui. En avançant dans cette voie, l’École de la République se mettra à l’abri de toute vision idéalisée du passé comme de l’avenir et de l’instrumentalisation de questions pédagogiques par les responsables politiques qui aboutit le plus souvent à des mouvements de balancier infondés et stériles. Cette voie permettra également de bâtir une véritable formation professionnelle liant connaissances théoriques et pratiques. Mais la finalité de tout cela est évidemment la réussite des élèves.
Estimer l’échec scolaire induit par le basculement de 1986
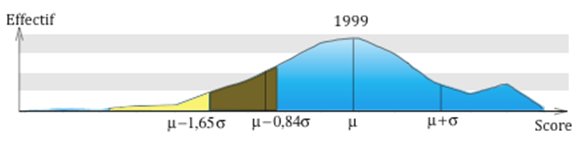
Pour estimer cet échec induit, posons-nous la question suivante : combien d’élèves de CM2, en 1999, passaient seulement pour des élèves faibles alors qu’ils auraient été considérés comme en très grande difficulté, voire « dyscalculiques », en 1987 ? On a une idée de la réponse en observant la courbe des performances des élèves en 1999.
On sait que, dans ce genre de passations, les scores se répartissent approximativement selon une courbe de Gauss caractérisée par la moyenne des scores (µ) et un indice de dispersion appelé écart-type (σ). Les élèves en grande difficulté en mathématiques sont ceux dont les scores figurent dans la partie gauche de la courbe. Mais à quelle frontière s’arrêter pour décider qui l’est ou ne l’est pas ? La limite est évidemment largement arbitraire mais il y a de bonnes raisons de retenir les élèves dont le score est inférieur à la moyenne de plus de 1,65 écart-type (Fischer, 2005). Cette population est proportionnelle à l’aire de la partie en jaune clair.
Pour estimer le nombre des élèves qui n’étaient pas considérés en situation de très grande difficulté dans leurs apprentissages numériques en 1999 alors qu’ils l’auraient été en 1987, il suffit d’imaginer la courbe de Gauss des performances en mathématiques en 1987. Il faut l’imaginer sur la droite de celle de 1999 ; sa moyenne est très exactement à 0,65 écart-type vers la droite (le fait que la partie décimale de ce nombre : 0,65σ, soit égale à celle du critère de décision retenu : – 1,65σ est un hasard complet). Comme l’écart type a augmenté dans un rapport de 1,19 entre 1987 et 1999, un calcul simple montre que lorsqu’on s’interroge sur les élèves de 1999 qui auraient été considérés comme en grande difficulté en 1987, ce sont ceux dont le score est inférieur à – 0,84σ de la moyenne et non à – 1,65σ qu’il faut retenir ; leur nombre est en nette augmentation ! Celle-ci est représentée sur la figure ci-dessous par l’aire de la partie brun foncé.
Il suffit dès lors de regarder la courbe et de connaître l’effectif global d’une génération d’élèves (un peu plus de 800 000 enfants), pour voir que la population des élèves de 1999 qui passaient seulement pour des élèves faibles alors qu’ils auraient été considérés comme en très grande difficulté, voire dyscalculiques, en 1987, est considérable, de plusieurs dizaines de milliers d’enfants, vraisemblablement plus de 100 000.
Que faut-il en conclure ? En premier lieu que pour la quasi-totalité de ces enfants, plutôt que d’être dyscalculiques, il vaut mieux dire avec Henri Canac qu’ils ont été « mal débutés » : le niveau que ces élèves ont atteint en CM2 n’était pas inscrit dans leurs gènes, il résulte en grande partie de l’importation imprudente en France de la culture pédagogique des États-Unis. En second lieu, il faut s’interroger sur ce qu’a été l’avenir de ces jeunes au collège. En effet, lorsque le niveau général baisse, les attentes des maîtres baissent également et on peut penser que ces élèves, en CM2, n’étaient pas trop malheureux. Cependant, objectivement, ils avaient un niveau qui, peu de temps auparavant, aurait été considéré comme celui d’élèves en très grande difficulté, un grand nombre d’entre eux auraient été diagnostiqués comme « dyscalculiques ». Qui peut penser qu’au collège leur parcours n’aura pas été celui de l’échec scolaire ?
Dans chaque génération d’élèves, le basculement de 1986 est vraisemblablement à l’origine de parcours d’échec en mathématiques se comptant par dizaines de milliers. Pour ces jeunes et pour leur famille, c’est un énorme gâchis humain. Pour le pays, cela représente un coût économique colossal : remboursement des prises en charge d’orthophonistes, défiscalisation des cours particuliers, redoublements, conséquences économiques et sociales à long terme. Pour les professeurs également, c’est beaucoup de déception et de souffrance. Or, l’École de la République dispose aujourd’hui de tout ce dont elle a besoin pour amorcer une refondation de la pédagogie des nombres et retrouver les performances qui étaient les siennes. Elle peut même espérer faire mieux que jamais.
Une chance historique de refonder la pédagogie des nombres : il faut la saisir
Nous avons la chance de pouvoir profiter des résultats de l’étude de 1986. Cette étude, en effet, a bénéficié de circonstances historiques exceptionnelles. Qui aurait pu imaginer qu’un jour, il serait possible de mener une sorte d’expérimentation à l’échelle de la nation ? Pour monter une expérimentation, en effet, il convient, de façon idéale, de disposer de 2 échantillons représentatifs de la population générale, l’un qui a appris dans une condition (absence d’enseignement du comptage numérotage) et l’autre dans l’autre condition (enseignement du comptage numérotage). Or, disposer de tels échantillons est a priori extrêmement difficile. En effet, enseigner le comptage numérotage correspond à ce que l’on peut appeler la « pédagogie selon le sens commun ». Trouver un échantillon représentatif des élèves français dont on est sûr que leurs enseignants de maternelle ne leur ont pas enseigné les nombres en utilisant la « pédagogie de sens commun » n’a rien d’évident. Or, la réforme des mathématiques modernes et les décisions radicales qui l’ont accompagnée (apprentissages numériques extrêmement tardifs) a fourni un tel échantillon : c’est celui des élèves qui, en 1987, ont participé à l’étude de la DEPP. De même, trouver un échantillon représentatif des élèves français dont on est sûr que leurs enseignants de maternelle leur ont effectivement enseigné précocement le comptage numérotage n’a rien d’évident : lorsqu’on a fait l’hypothèse que cela se traduira par une dégradation des performances, y procéder pose des problèmes de déontologie. Or, le basculement de 1986 et le changement de culture pédagogique qui l’a accompagné (importation de la culture pédagogique des États-Unis) a fourni un tel échantillon : c’est celui des élèves qui, en 1999, ont participé à l’étude de la DEPP. Tout s’est passé comme si, par deux fois, la nation avait décidé des changements culturels rendant possible une telle expérimentation ! On n’est pas près de revivre de telles circonstances historiques.
Nous avons la chance que la comparaison ait conduit à des résultats extrêmement clairs (une dégradation manifeste) avec un grand nombre de contrôles possibles permettant de s’assurer que la cause des performances moindres en 1999 est bien d’ordre pédagogique.
Nous avons la chance qu’une étude détaillée des causes pédagogiques possibles conduise à un diagnostic invitant à sortir du débat stérile entre « enseignants républicains » et « pédagogues ». Comme l’origine de la dégradation se situe en 1986 et non en 1970, les premiers doivent s’interroger sur ce qu’étaient réellement les pratiques pédagogiques anciennes. Par ailleurs, le bonheur que procure la lecture des textes des pédagogues du milieu du 20e siècle doit conduire ceux qui se considèrent modernes à réévaluer ces écrits. Les uns et les autres sont susceptibles de se rapprocher : il est souvent plus facile de renouer le dialogue lorsqu’il est avéré que personne ne peut camper sur ses positions.
Nous avons la chance que le diagnostic qu’il faut avancer se formule avec autant de clarté : Mathieu ne sait pas calculer parce qu’à l’école, il apprend à compter comme Matthew qui, lui-même, apprend très mal à calculer. Nous avons la chance qu’un tel diagnostic évoque immédiatement une issue : renouer avec la culture pédagogique qui était celle des pays francophones avant le basculement de 1986.
Nous avons la chance qu’un tel traitement ne conduise pas seulement à la préconisation de revenir aux pratiques pédagogiques d’il y a 50 ans : rien n’est plus désespérant pour un professeur d’écoles que d’avoir l’impression de devoir faire ce qui se faisait il y a 50 ans et qui a été rejeté il y a 25 ans. Il n’est pas question aujourd’hui de dire aux enseignants : « Ne faites plus compter vos élèves à l’école ». Mais plutôt : « Attention, il y a deux formes de comptage, l’une fait obstacle au progrès vers le calcul, l’autre le favorise ; il y a une façon simple de distinguer ces deux façons d’enseigner le comptage… ». Il n’est pas question de leur dire : « Bannissez tout usage des constellations du dé de votre classe », mais plutôt : « Attention ces configurations peuvent fonctionner de manière numérique ou non ; il y a une façon de savoir ce qu’il en est… ». Il n’est pas question de dire aux enseignants : « Empêchez vos élèves d’utiliser leurs doigts pour résoudre un problème numérique », mais plutôt : « Attention, il y a deux façons d’utiliser les doigts, l’une fait obstacle au progrès vers le calcul, l’autre le favorise ; il y a une façon simple de distinguer ces deux façons… ».
Nous avons la chance qu’une meilleure connaissance des différentes façons de parler les nombres aux enfants de 2 – 4 ans ouvre une perspective de démocratisation de l’accès à de bonnes connaissances numériques initiales qui sont la condition sine qua non de la réussite ultérieure en mathématiques.
Nous avons la chance que, sous les ministres Robien-Darcos-Chatel, une sorte de mouvement de résistance pédagogique se soit développé, impliquant IEN, conseillers pédagogiques et de nombreux professeurs d’écoles, à moins qu’il ne s’agisse plus simplement d’un mouvement de « réalisme professionnel » venant du terrain confronté à des problèmes sérieux avec de nombreux élèves. Ces professionnels ont permis que des pratiques pédagogiques efficientes s’élaborent et qu’elles puissent être aujourd’hui rassemblées et développées.
Nous avons la chance que la refondation de l’école soit aujourd’hui à l’ordre du jour parce que le changement de majorité rend possible une authentique formation professionnelle permettant d’outiller les enseignants sur les plans historique, conceptuel, technique et de les aider à adopter une posture réflexive. On imagine mal, en effet, qu’il soit possible de reconstruire la culture pédagogique évoquée dans ce texte, sans un développement important de la formation professionnelle initiale et continue.
Nous avons toutes ces chances et nous passerions à côté ?
Rémi Brissiaud
Laboratoire Paragraphe – Université Paris 8
Bibliographie
Bandet, J. (1962) Les débuts du calcul. Paris : Bourrelier.
Baroody A. Bajwa, N. & Eiland M. (2009) Why Can’t Johnny Remember the Basic Facts ? Developmental disabilities research reviews ; 15, 69-79.
Brachet, F., Canac, H. & Delaunay E. (1955) L’enfant et le nombre. Didier, Paris.
Brissiaud R. (1989a) Comment les enfants apprennent à calculer. Paris : Retz
Brissiaud R. (1989b) : Compter à l’école maternelle. Oui, mais… Bulletin de l’Association des Professeurs de Mathématiques de l’Enseignement Public ; 367, 31-52.
Brissiaud R. (1990) Calculer et compter de la PS à la GS de maternelle. Revue Grand N, 49, p. 37-48
Brissiaud, R. (1991). « Un outil pour construire le nombre : les collections-témoins de doigts », in J. Bideaud, C. Meljac & J.-P. Fischer (éd.), Les chemins du nombre, p. 59-90. Lille : Presses universitaires.
Brissiaud, R. (1995a) Le comptage en tant que pratique verbale : un rôle ambivalent dans le progrès des enfants. Repères, 12, p. 120-143.
Brissiaud R. (1995b) Enseignement et développement des représentations numériques chez l’enfant. Thèse de psychologie. Université Paris 8
Brissiaud, R. (2007) Premiers pas vers les maths. Les chemins de la réussite à l’école maternelle. Paris : Retz.
Brissiaud, R. & Sander, E. (2010). Arithmetic word problem solving : a Situation Strategy First
framework. Developmental Science, 13 (1), 92-107.
Brousseau, G. (1972) Processus de mathématisation. Bulletin de l’APMEP, 57-84
Canac, H. (1955) L’initiation au calcul entre 5 et 7 ans. In F. Brachet, H. Canac & E. Delaunay (ed.), L’enfant et le nombre, p.9-27. Paris : Didier.
Davidson, K., Eng, K. & Barner, D. (2012) Does learning to count involve a semantic induction? Cognition ; 123-1 ; p. 162-173.
Dehaene, S. (1997-2010) La bosse des maths – 15 ans après. Paris, Odile Jacob.
Droz, R. & Paschoud, J. (1981) : Le comptage et la procédure « (+1)-itérée » dans l’exploration intuitive de l’addition. Revue Suisse de Psychologie, 40, 219-237.
Ermel (1990) Apprentissages numériques, cycle des apprentissage, Grande Section de maternelle. Paris : Hatier.
Fareng R. & Fareng, M. (1966) Comment faire ? L’apprentissage du calcul avec les enfants de 5 à 7 ans. Paris, Fernand Nathan.
Fischer, J.-P. (1991). Le subitizing et la discontinuité après 3, in J. Bideaud, C. Meljac & J.-P. Fischer (éd.), Les chemins du nombre, p. 235-258. Lille : Presses universitaires.
Fischer, J.P. (1992) Les apprentissages numériques. Nancy, Presses Universitaires de Nancy
Fischer J.-P., 2005. Le diagnostic de dyscalculie à partir de l’évaluation en CE2 : vers une approche scientifique ? Nouvelle Revue de l’AIS, 32, 85-98.
Fischer, J. P. (2010). Vers une levée du mystère des écritures en miroir (des chiffres) chez l’enfant, L’Année psychologique, 110, 227-251.
Fuson, K.C. (1988). Children’s counting and concepts of number. New York : Springer.
Fuson K.C. & Kwon Y. (1991) Systèmes de mots-nombres et autres outils culturels : effets sur les premiers calculs de l’enfant. In J. Bideaud, C. Meljac & J.-P. Fischer (éd.), Les chemins du nombre, p. 351-374. Lille : Presses universitaires
Fuson K.C. & Kwon Y. (1992) : Korean children’s single-digit addition and substraction: numbers structured by ten. Journal for Research in Mathematics Education, 23 (2), 148-165.
Geary, D.C. (2005) Les troubles d’apprentissage en arithmétique : rôle de la mémoire de travail et des connaissances conceptuelles. In M.-P. Noël (Ed) : La dyscalculie. Marseille : Solal.
Geary D.C., Fan L. & Bow-Thomas C.C. (1992). Numerical cognition: Loci of ability differences comparing children from China and the United States. Psychological Science, 3,180-185.
Gelman R. & Gallistel C.R. (1978). The child’s understanding of number. Cambridge : Harvard University Press.
Gelman, R. (1983) Les bébés et le calcul, La Recherche, n°14 (149), p. 1382-1389.
Hodent, C., Bryant, P., & Houdé, O. (2005) Language-specific effects on number computation in toddlers. Developmental Science 8 (5), 420–423.
Labat, H., Ecalle, J., & Magnan, A. (2010). Effet d’entraînements bi-modaux à la connaissance des lettres. Etude transversale chez des enfants de 3 et 5 ans. Psychologie Française, 55(2), 113-127.
Markman, E.M. (1989) : Categorisation and naming in children. Cambridge, MA: MIT Press. Markman, E.M. (1990) : Constraints children place on word meanings. Cognitive Science, 14, 57-77
MEN (1986). L’école maternelle, son rôle, ses missions. CNDP
MEN/DGESCO (2010) Aide à l’évaluation des acquis des élèves en fin d’école maternelle – Découvrir le monde – Ressources pour faire la classe à l’école. Document mis en ligne sur le site eduscol.
Mialaret, G. (1955) Pédagogie des débuts du calcul. Fernand Nathan, Paris (avec la collaboration de l’Unesco).
Palanque R., Cambrouse E. & Loubet E. (1987) Prépa-math – Maternelle/grande section – Dossier pédagogique. Paris : Hachette.
Piazza, M., Fumarola, A., Chinello, A. & Melcher, D. (2011) Subitizing Reflects Visuo-spatial Object Individuation Capacity. Cognition, 121(1):147-153.
Rocher T. (2008) Lire, écrire, compter : les performances des élèves de CM2 à vingt ans d’intervalle 1987-2007. Note 08.38 de la DEPP ; décembre 2008.
Sarnecka, B.W. & Carey, S. (2008). How counting represents number: What children must learn and when they learn it. Cognition, 108(3), 662-674.
Savard, C. (1940) Pages choisies de pédagogie contemporaine. Paris : Delagrave.
Schaeffer, B., Eggleston, V.H. & Scott, J.-L. (1974). « Number development in young children », Cognitive Psychology, 6, p. 357-379.
Siegler, R. S., & Ramani, G. B. (2009). Playing linear number board games — but not circular ones –improves low-income preschoolers’ numerical understanding. Journal of Educational Psychology, 101, 545-560.
Sinclair, H., Bamberger, J., Ferreiro, E., Frey-Streiff, M. & Sinclair, A. (1988). La production de notations chez le jeune enfant : Langage, nombres, rythmes et mélodies. Paris : PUF