Les premiers apprentissages mathématiques prédisent la réussite ou les difficultés scolaires à venir. Le Café pédagogique publie en avant-première une série de 3 textes de Rémi Brissiaud (Paris 8) adaptés d’un livre à paraître début décembre aux éditions Retz. Il montre que la brutale dégradation des performances en calcul constatée en 1999 par la DEPP (et confirmée depuis) n’est pas une conséquence de la réforme des mathématiques modernes de 1970 parce qu’elle se produit bien plus tard, après les instructions officielles de 1986. En revanche, cette réforme nous a fait oublier ce qu’était notre culture pédagogique des premiers apprentissages numériques. Cela a facilité, en 1986, un basculement vers des pratiques pédagogiques qui appartiennent à une autre culture : celle des États-Unis, un pays dont la langue, l’anglais, est très différente et qui n’a pas d’école maternelle. Il montre que ce basculement est à l’origine de l’effondrement des performances en calcul et il alerte : ce que certains mettent en avant aujourd’hui « davantage de ludique, moins de symbolique » résoudrait peut-être le problème de la primarisation de l’école maternelle, qui est réel, mais cela empêcherait notre école de renouer avec la culture pédagogique qui était la sienne et cela pérenniserait l’échec scolaire. Pour Rémi Brissiaud, l’École de la République risque de passer à côté de la possibilité de refonder la pédagogie des nombres alors qu’elle dispose de tous les outils pour le faire.

Un premier objectif de ce texte est de montrer, à partir d’une analyse des données conduisant au diagnostic d’une baisse brutale des performances à partir des années 1990, que la pédagogie des nombres doit être repensée dès l’école maternelle ; elle nécessite même une véritable refondation ; un simple replâtrage de tel ou tel aspect des pratiques pédagogiques actuelles, serait inefficace. Et cette refondation doit être celle de la culture pédagogique au sens où l’école maternelle doit renouer, concernant les apprentissages numériques, avec la culture pédagogique qui était la sienne depuis 1923 environ et jusqu’en 1986. En effet, il sera montré qu’au niveau de l’école maternelle et du début de l’élémentaire, c’est pour l’essentiel la continuité qui prévaut entre 1923 et 1986. Entre ces deux dates, il y eut bien la réforme de 1970, celles des « mathématiques modernes », mais elle n’a pas créé la rupture que certains croient : ce qui apparaissait fondamental aux pédagogues avant 1970, est resté traduit dans les pratiques après cette date. En revanche, après la publication en 1986 d’une circulaire concernant l’école maternelle, les élèves se sont mis à apprendre en France comme aux États-Unis, un pays qui ne possède pas d’institution équivalente à notre école maternelle et dont la langue, l’anglais, favorise bien mieux l’accès au nombre que la nôtre. Cette circulaire était signée Jean-Pierre Chevènement mais, en l’occurrence, il a agi à rebours de ce qu’il croyait faire. Les conséquences de ce basculement doivent être reconsidérées aujourd’hui.
Un second objectif est de montrer qu’un autre changement politique s’impose aujourd’hui : il faut que, concernant la pédagogie des apprentissages numériques à l’école (et probablement dans d’autres domaines), le ministère rompe avec un mode de gestion plus soucieux de diffuser les supposées « bonnes pratiques », instituant ainsi une sorte de pédagogie officielle, que d’outiller les enseignants sur les plans historiques, conceptuels, techniques et réflexifs. La reconstitution d’une culture pédagogique des premiers apprentissages numériques est une condition nécessaire pour que les enseignants aient des pratiques pédagogiques adaptées à leurs élèves.
La baisse des performances et le « basculement de 1986 »
Rappelons d’abord que c’est entre 1987 et 1999 que les performances en calcul des écoliers français se sont fortement dégradées. Thierry Rocher (note 08.38 de la DEPP ; décembre 2008) a montré qu’entre ces deux dates, la moyenne des élèves de CM2 baisse des 65% de l’écart-type initial. Pour avoir une idée de ce que cela représente, il suffit de noter qu’en se basant sur le dispositif EIST et sur PISA, études menées au collège et au Lycée, on observe que le bénéfice d’une année d’apprentissage (entre la 6e et la 5e et entre la 3e et la 2nde) est de 40-50% de l’écart-type initial ; ce bénéfice est à comparer avec la baisse de 65% à un même niveau de classe entre 1987 et 1999. En revanche, les performances se stabilisent à ce bas niveau entre 1999 et 2007.
À la recherche des causes de la baisse
Face à de tels résultats, il convient évidemment d’examiner de manière assez précise la méthodologie utilisée : n’y aurait-il pas un biais dans le traitement statistique utilisé ? Par exemple : l’étude se base sur des épreuves communes mais celles-ci ne le sont qu’aux passations de 1987 et 2007, la comparaison de 1987 et 1999 se faisant, elle, par une méthode statistique appelée la triangularisation. Ayant eu un échange avec Thierry Rocher, il est formel : si on refait les traitements statistiques en introduisant des conditions très défavorables à l’hypothèse d’une baisse, les résultats restent si nets que, dans tous les cas, il faut considérer que l’on est face à une sorte d’effondrement des performances.
Or cette étude a bénéficié de circonstances historiques exceptionnelles qui font qu’elle est extrêmement riche d’enseignements (Brissiaud, 2012). Elle infirme par exemple ce que Luc Chatel avançait comme explication lors d’une intervention au Sénat, en mars 2011 : « Pendant de nombreuses années, en conséquence sans doute de Mai 68, notre système éducatif a en effet oublié qu’enseigner, c’est d’abord transmettre des savoirs… ». Elle infirme également ce que pensaient quelques académiciens des sciences qui, dans une lettre au ministre du 25 janvier 2007, soulignaient l’urgence qu’il y aurait eu « d’inverser le mouvement de régression entamé depuis les années 1970 ». La date de 1970 n’est pas un hasard : c’est celle d’entrée en vigueur des programmes de l’école primaire qui marquent le début de la « réforme des mathématiques modernes ». On se rappelle mal aujourd’hui le phénomène social que fut cette réforme. Elle est notamment à l’origine du samedi après-midi libéré pour les enfants mais studieux pour les instituteurs : ils devaient le consacrer à se « recycler » en mathématiques modernes (à l’époque, les sessions de formation continue s’appelaient des « stages de recyclage »). Dès 1970, de très grands mathématiciens, dont René Thom, avaient été très hostiles à cette réforme, et les académiciens qui, en 2007, s’adressaient ainsi au ministre, ne faisaient que s’inscrire dans cette continuité : de leur point de vue, la baisse des performances en calcul était la preuve que cette réforme n’aurait jamais dû avoir lieu.
Or, le diagnostic du ministre, comme celui de ces académiciens, était erroné : en 1987, près de 20 ans après Mai 68, 17 ans après la réforme des maths modernes (1970), les élèves calculaient encore bien. Là encore, pour donner une idée de ces performances, on peut noter qu’une multiplication telle que 247 x 36 était réussie par 84% des élèves de CM2 en 1987 ; l’addition en colonnes de trois nombres 19 786 + 215 + 3 291 était réussie par 94% de ces mêmes élèves (Rocher, 2008). Dans un cas comme dans l’autre, il sera difficile de faire mieux à l’avenir parce que de tels taux de réussite sont élevés et, à partir d’un certain score, il est difficile de progresser encore (on appelle cela un « effet plafond »). En 1987, les élèves calculaient encore bien et ce serait déjà un beau progrès de retrouver les performances d’alors. En 2007, en effet, le taux de réussite à la même multiplication n’est que de 68% (84% auparavant) et celui de la même addition de 83% (94% auparavant) : même les additions, une opération dont les élèves de CM2 répètent l’exécution depuis bien longtemps, sont moins bien réussies. Mieux valait être un élève apprenant le calcul dans les 20 années ayant suivi Mai 68 et les 17 années ayant suivi la réforme des mathématiques modernes qu’un élève d’aujourd’hui. Comme nous allons le voir, cette erreur de diagnostic des académiciens a rendu singulièrement difficile l’émergence d’un autre diagnostic, permettant, lui, d’expliquer la forte dégradation des performances en calcul.
De plus, l’étude de la DEPP permet d’exclure toutes les causes de la baisse qui viennent à l’esprit et qui ne sont pas d’ordre pédagogique. La dégradation des conditions sociales de certains enfants, suite au phénomène de ghettoïsation des banlieues pourrait-il l’expliquer ? Non, la baisse affecte tous les milieux socioculturels dans les mêmes proportions, les enfants d’ingénieurs comme ceux de chômeurs. L’augmentation du temps passé devant la télé ou la console de jeu pourrait-il l’explique? Non, sur la même période, il n’y a pas de baisse des performances en français et on comprendrait mal qu’un tel phénomène affecte de manière spécifique le calcul. Et une éventuelle baisse des moyens accordés à l’école ? La période 87-99 est, tout au contraire, la dernière durant laquelle les moyens accordés à l’école ont été revalorisés de manière considérable : le statut et la rémunération des professeurs d’écoles est aligné sur celui des certifiés, une formation professionnelle conséquente, etc. Cela ne signifie évidemment pas que l’école pourra redevenir performante sans de nouveaux moyens : ceux-ci se sont considérablement dégradés depuis l’année 2000 environ et on peut sérieusement douter que la mobilisation nécessaire pour revenir aux performances antérieures soit possible avec un statu quo. Mais l’analyse des résultats de la DEPP prouve que, dans le domaine du calcul, une amélioration des moyens accordés à l’école peut tout aussi bien aboutir à la situation de 1999 (performances dégradées) qu’à celle de 1987 (bonnes performances). L’amélioration des moyens est nécessaire. Elle n’est pas suffisante.
On en vient donc à envisager les causes d’ordre pédagogique. Cela conduit à comparer les pratiques pédagogiques de la période 1970-1987 avec celles de la période qui suit (1987-2007). En fait, nous commencerons effectivement par comparer ces deux période mais, dans un deuxième temps, nous verrons que c’est la période 1923-1986 qu’il faut comparer avec la période qui suit (1987-2007). En effet, comme on va le montrer, la réforme de 1970, que certains considèrent comme un bouleversement, s’est en réalité effectuée en préservant ce qui était au cœur de la culture française des premiers apprentissages numériques. De plus, pour une meilleure intelligibilité, c’est 1986, et non 1987, qui sera retenue comme date charnière, parce que c’est en 1986 que paraît un texte officiel qui institutionnalise un basculement de la pédagogie du nombre à l’école maternelle.
Le « basculement de 1986 »
Entre 1970 et 1986, suite aux travaux de Piaget, les pédagogues doutaient que les enfants puissent profiter d’un enseignement des nombres avant 6-7 ans et, à l’école maternelle, l’accent était mis sur des activités qualifiées de « pré numériques ». Les enseignants distribuaient par exemple à leurs élèves des blocs en PVC de formes, tailles, épaisseurs et couleurs différentes et les enfants devaient trouver tous les triangles rouges, puis les triangles rouges épais. Ils avaient aussi à mettre en série des tiges de tailles différentes, etc. Le comptage n’était d’aucune façon préconisé et jamais un enseignant n’aurait fait compter ses élèves le jour de la visite de l’inspecteur. Qui se souvient encore que dans le Monde de l’Éducation de novembre 1982, on pouvait lire : « Pour des enfants de cinq ans, apprendre à compter jusqu’à dix n’a guère d’utilité (sinon faire plaisir aux parents) » ? Dans le fichier le plus utilisé au CP, la leçon sur les nombres 1, 2 et 3 se situait en novembre et les élèves n’écrivaient le nombre 10 qu’en janvier. Ce sont ces élèves qui, arrivés en CM2 en 1987, calculaient bien.
Cette période s’achève en 1986 avec la publication d’une circulaire sur l’école maternelle (MEN, 1986). On y lit : «Progressivement, l’enfant découvre et construit le nombre. Il apprend et récite la comptine numérique ». Après plus de 15 ans de quasi disparition de tout apprentissage numérique à l’école maternelle, sous l’ère piagétienne, le changement était radical. C’est pour cela que l’on parlera dans la suite de ce texte du « basculement de 1986 ». Dans un ouvrage (Palanque et col, 1987), une professeure de mathématiques raconte comment, après la lecture dans la revue « La Recherche » d’un article de vulgarisation d’une psychologue américaine, Rochel Gelman (1983), ses collègues d’une équipe liée à l’INRP, Ermel, (Équipe de Recherche Mathématiques à l’école Élémentaire) effectuent une volte-face dans leurs convictions. Il est vrai que l’article s’intitulait : « Les bébés et le calcul » et que, si les bébés savent calculer, il devient difficile de justifier l’absence de tout apprentissage numérique à l’école maternelle.
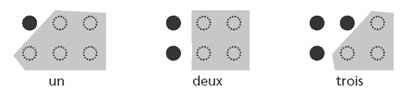
Les mathématiciens de Ermel se mettent à penser que le comptage doit être enseigné le plus tôt possible (dès la petite section) et ils décident de l’enseigner en attirant l’attention des élèves sur ce que Rochel Gelman appelait le « principe de correspondance terme à terme » (Gelman & Gallistel, 1978) : lorsqu’on compte, l’enfant qui réussit doit être attentif à faire correspondre 1 mot avec 1 objet ; on dit « Un (un objet est pointé), deux (un autre objet est pointé), trois (encore un autre)… ». Il est important de souligner que cette manière de compter « à la Gelman » est aussi celle que les parents adoptent le plus souvent en dehors de l’école : le basculement de 1986 ne correspond donc pas seulement à l’importation de la culture pédagogique des États-Unis, c’est aussi l’importation, au sein de l’école maternelle, de la pédagogie du comptage selon le sens commun. Le plus souvent aujourd’hui, les enfants de PS apprennent à compter ainsi jusqu’à 5. Dans presque toutes les GS, une file numérotée est affichée jusqu’à 30. On compte ainsi presque tous les jours les enfants présents, les étiquettes des absents. Quand un enfant ne sait pas écrire le chiffre 8, il compte ainsi jusqu’à ce nombre sur la file numérotée afin d’en retrouver l’écriture chiffrée. Aujourd’hui encore (octobre 2012), sur le site du ministère, eduscol, figure une épreuve d’évaluation de fin de GS et, quand un élève échoue un comptage jusqu’à 30, il est recommandé au maître d’attirer fortement l’attention de cet élève sur la correspondance 1 mot – 1 objet (MEN/DEGESCO, 2010). Ce sont ces élèves qui, arrivés en CM2, calculent mal.
Depuis 1986, avec des apprentissages numériques aussi précoces, les élèves devraient devenir bien meilleurs en calcul que leurs prédécesseurs ! L’étude de la DEPP montre que c’est le contraire qui est vrai. On se trouve donc face à un paradoxe : comment se fait-il qu’à une époque où l’école enseignait les nombres beaucoup plus tardivement, elle formait des élèves bien plus performants en calcul qu’aujourd’hui ? Nous allons voir que l’enseignement du comptage « à la Gelman » éloigne les élèves du calcul plus qu’il ne les en rapproche.
Mais le basculement de 1986 concernant les apprentissages numériques aux cycles 1 et 2 (école maternelle, CP et CE1) n’est peut-être pas le seul changement pédagogique qu’il convient d’étudier pour comprendre l’effondrement des performances en calcul. Comme c’est au niveau du CM2 que l’étude de la DEPP compare les performances des élèves de 1987 et de 1999, une explication possible serait qu’avant 1987, les maîtres de cycle 3 (CE2, CM1, CM2) avaient des pratiques pédagogiques bien meilleures que ceux qui leur ont succédé. Si c’est le cas, il faut absolument essayer de préciser quelles sont ces pratiques pédagogiques : elles permettraient en effet aux élèves d’être bien plus performants qu’aujourd’hui en commençant l’apprentissage beaucoup plus tardivement et, donc, en y consacrant beaucoup moins de temps.
En fait, personne encore n’a pris l’initiative de défendre un tel point de vue. En effet, cette période 1970-1987 recouvre grandement celle des « mathématiques modernes » et un grand nombre des activités menées à l’époque (le calcul en bases autres que 10, par exemple) ont été très critiquées. On peut rappeler également qu’entre 1970 et 1990, le signe de la soustraction (le symbole « – ») n’était introduit que vers le milieu du CE1 (seule l’addition à trou était étudiée au CP et en début de CE1). Faut-il voir dans cette introduction tardive du signe de la soustraction, l’une des raisons des meilleurs résultats ? Peu de gens sont prêts à défendre cette idée.
Bien plus probablement, c’est un phénomène ayant affecté les premiers apprentissages numériques (cycles 1 et 2) qu’il convient d’incriminer, à savoir le basculement qu’à représenté, à partir de 1986, la préconisation d’enseigner le comptage « à la Gelman » aux jeunes élèves.
Les progrès que permet le comptage « à la Gelman », ceux qu’il ne permet pas
Enseigner le comptage « à la Gelman », c’est enseigner un comptage numérotage
En fait, enseigner le comptage « à la Gelman » ou selon le sens commun est loin de permettre aux enfants d’accéder facilement au nombre. Ainsi, en PS et en MS, on observe très fréquemment le dialogue suivant (Schaeffer & col, 1974) :
Adulte : Combien y a-t-il de jetons ?
Enfant (en comptant les jetons) : « un », « deux », « trois », « quatre ».
Adulte : Oui, alors combien y a-t-il de jetons ?
Enfant (recompte les jetons) : « Un », « deux », « trois », « quatre ».
Adulte : Je suis d’accord, mais ce que je t’ai demandé, c’est combien il y a de jetons ?
Enfant (recompte encore) : « Un », « deux », « trois », « quatre ».
Cet enfant met bien en correspondance terme à terme les mots-nombres et les jetons de la collection, mais il n’isole pas le dernier mot-nombre prononcé pour répondre à la question posée. L’enfant reste apparemment incapable d’exploiter ce comptage pour répondre à la question : « Combien… ? ». Son comptage ne lui permet pas d’accéder au nombre. On peut dire : son comptage n’est pas un dénombrement.
Pour comprendre ce phénomène, il suffit d’imaginer un autre contexte où l’enfant pointe des objets en disant des mots tous différents : « cube », « table », « fenêtre », « toboggan », par exemple. Le dernier mot prononcé, « toboggan », réfère à l’objet qui est pointé au moment où ce mot est prononcé (le toboggan), il ne dit rien des autres objets, ni de l’ensemble des objets. Or, lors d’un comptage « à la Gelman », le dernier mot, « quatre », est prononcé alors que l’enfant pointe le dernier objet, comme dans l’exemple précédent, mais dans ce cas l’enfant devrait comprendre que « quatre », pour l’essentiel, ne réfère pas à cet objet parce qu’il désigne une propriété de l’ensemble des objets : ce mot précise quelle est la pluralité que l’enfant a devant lui, il dit le nombre d’unités de la collection. Pointer un objet tout en prononçant un mot, alors que celui-ci désigne pour l’essentiel une propriété d’autre chose, correspond à un fonctionnement du langage complètement atypique (Markman, 1989 ; 1990). À vrai dire, on ne l’observe que dans le contexte de l’enseignement du comptage « à la Gelman ». C’est donc l’insistance des pédagogues sur la correspondance 1 mot – 1 élément qui explique l’incompréhension des enfants : elle les conduit à concevoir les éléments successivement pointés comme « le un, le deux, le trois, le quatre… ». Les mots prononcés sont alors des sortes de numéros renvoyant chacun à un élément et un seul ; le dernier mot prononcé est lui aussi un numéro, comme les autres.
Ainsi, enseigner le comptage « à la Gelman », selon la pédagogie de sens commun, c’est enseigner un comptage numérotage (Brissiaud, 1989a). Les preuves empiriques en sont nombreuses : lorsque des enfants de 4 ans et demi environ viennent de compter 7 objets et lorsqu’on leur demande de montrer les 7 objets, en insistant sur la marque du pluriel (les), les enfants montrent quand même un seul objet : le dernier pointé (Fuson, 1988) ; lorsqu’on demande à des élèves de GS de rédiger un message écrit afin de ne pas oublier combien il y a d’objets dans une collection de 7 objets qu’ils viennent de compter, ils dessinent : 1, 2, 3, 4, 5, 6, 7, c’est-à-dire l’ensemble des numéros qu’ils viennent d’utiliser (Sinclair & col, 1988 ; Brissiaud, 1989a). Pour comparer deux collections, certains enfants comptent l’une en disant : 1, 2 , 3, 4 ; puis l’autre collection en disant : 1, 2 , 3, 4, 5 et ils concluent correctement alors qu’ils ne savent pas répondre 4 et 5 à la question « Combien y a-t-il… ? » : ils ont compris que lorsque leur comptage numérotage va plus loin, on peut dire : « Il y a plus là que là » (Droz & Paschoud, 1981).
Cette signification des mots-nombres s’installe d’autant plus facilement que les jeunes enfants vivent dans un univers de numéros : en dehors de l’école, 4 est pour les enfants le numéro de l’étage où ils habitent, 28, celui de leur appartement, 3 celui de la chaîne télé… Lorsqu’un enfant appuie sur la touche « 3 » de la télécommande, il ne voit pas 3 images, il voit une seule image, celle de « la 3 ». Bref, un enseignement précoce du comptage « à la Gelman » renforce la signification des mots-nombres en tant que numéros et ne favorise pas l’accès à leur signification en tant que noms de nombres, lorsqu’ils désignent des pluralités.
Les exemples précédents montrent que l’usage du comptage numérotage permet certains progrès ; il permet même la comparaison de la taille de 2 collections. Cependant, ces quelques progrès risquent de se payer au prix fort ultérieurement car l’enseignement du comptage numérotage éloigne les élèves du calcul. En effet, la relation numérique « 5 et encore 3, c’est 8 » n’a aucun sens lorsqu’on interprète les chiffres comme des numéros. Regarder successivement les programmes de « la 5 » puis de « la 3 », ne dit rien de ceux de « la 8 ». L’entrée dans le calcul est évidemment impossible tant que les enfants n’ont pas compris que les mots qu’ils utilisent pour compter désignent des pluralités successivement engendrées par l’ajout d’une unité : « deux, c’est un et encore un » ; « trois, c’est un, un et encore un » ou bien : « trois, c’est deux et encore un ».
Faire le choix du comptage numérotage, c’est contraindre les enfants à s’approprier les nombres et le calcul alors que l’on fait un usage des mots qui masque ce qu’il est crucial d’apprendre, c’est contraindre les enfants à un apprentissage implicite des nombres et du calcul. L’entrée dans le calcul est alors une telle course d’obstacles que les élèves les plus fragiles y échouent en grand nombre. Toutes les études sur les enfants en difficulté grave et durable, ceux que certains chercheurs qualifient de « dyscalculiques », décrivent ces enfants comme enfermés dans le comptage 1 à 1 (Geary, 2005).
C’est la raison pour laquelle, dans la culture pédagogique française, depuis 1923 environ jusqu’au basculement de 1986, l’enseignement du comptage numérotage avait été d’abord très sévèrement critiqué, puis proscrit. La raison avancée était que « … cette façon empirique fait acquérir à force de répétitions la liaison entre le nom des nombres, l’écriture du chiffre, la position de ce nombre dans la suite des autres, mais elle gêne la représentation du nombre, l’opération mentale, en un mot, elle empêche l’enfant de penser, de calculer » (Fareng & Fareng, 1966). On retrouve dans cette citation les idées qui viennent d’être exposées : il est vrai que des progrès sont possibles avec un enseignement précoce du comptage numérotage ; mais, chez de nombreux élèves, cette façon d’enseigner le comptage provoque surtout un retard dans l’appropriation du calcul.
On peut aussi évoquer Henri Canac (1955), sous-directeur de l’ENS de Saint-Cloud et membre de la commission Langevin-Wallon. Évoquant ces enfants qui, au cours moyen, sont incapables de retrouver le résultat d’une addition élémentaire sans compter 1 à 1, il les qualifient d’« élèves mal débutés ». L’étude de la DEPP valide ce que pensaient ces pédagogues d’avant 1970 et va même au-delà : mieux vaut ne rien enseigner du tout à l’école maternelle plutôt que d’y créer de tels obstacles au progrès (nous verrons qu’il faudrait préciser : surtout lorsqu’on parle français, parce que cela est moins vrai lorsqu’on parle anglais).
Une autre possibilité : enseigner les décompositions et le comptage dénombrement
Mais l’absence de tout apprentissage numérique à l’école maternelle, comme ce fut le cas entre 1970 et 1986, n’est pas la seule solution pédagogique, ni vraisemblablement la meilleure. Il existe une autre façon de parler les nombres à l’école maternelle, notamment, en PS et en MS (Brissiaud, 1989 ; 2007).
Elle consiste, dans un premier temps, à éviter tout enseignement du comptage numérotage et même, plus généralement, à éviter toute utilisation par l’enseignant des mots-nombres en tant que numéros, afin de privilégier les décompositions des 3 premiers nombres. Ainsi, pour enseigner le nombre 2, l’enseignant de PS utilise comme synonyme de deux : « un et encore un », en faisant, bien sûr, les actions correspondantes : « Deux cubes, c’est un cube (l’enseignant prend 1 cube) et encore un (il en prend 1 autre), deux (ils les montrent tous les deux) » ; et il demande à l’enfant de donner de même : « deux crayons, un crayon et encore un », deux petites voitures… Il ne dit donc jamais : « un, deux » en pointant successivement les objets, il ne les numérote jamais. Puis, quand les enfants ont compris les nombres 1 et 2, il fait de même avec le nombre 3 en utilisant comme synonyme de trois : « un, un et encore un » ou bien « deux et encore un ».
C’est seulement lorsque les enfants ont une connaissance approfondie des 3 premiers nombres qu’il devient possible d’enseigner le comptage. Avoir cette connaissance approfondie, c’est réussir tout un ensemble de tâches mettant en jeu ces nombres : savoir dire directement ces nombres en face d’une collection correspondante ; savoir donner une collection ayant 1, 2 ou 3 éléments ; savoir reconnaître directement une collection de 3 parmi des collections de 2 et 4 ; savoir résoudre des problèmes où il s’agit d’anticiper le résultat d’ajouts et de retraits de 1 ou 2 dans le tout petit domaine numérique des 3 premiers nombres, etc.
Dès que les élèves ont une connaissance approfondie des 3 premiers nombres, donc, il devient possible d’enseigner le comptage d’abord jusqu’à 4, plus tard jusqu’à 5. Et il est nécessaire et très facile que cet enseignement prenne une forme différente du comptage numérotage. Décrivons cette autre façon de l’enseigner en se plaçant dans la situation où, pour donner 4 cubes à un nounours, par exemple, l’enseignant montre aux élèves comment on compte des objets en les prélevant successivement d’un stock. L’enseignant dit « un » quand il a déplacé le 1er objet, il dit « deux » non pas au moment où il touche le 2e objet, mais quand celui-ci a été déplacé et, donc, quand la collection des deux objets a été formée (on vise à ce que l’enfant associe le mot « deux » à la pluralité : 2, c’est le résultat de 1 et encore 1), il dit « trois » non pas au moment où il touche le 3e objet mais au moment où celui-ci a été déplacé et, donc, quand la collection de trois objets a été formée (pour que l’enfant associe le mot « trois » à la pluralité : 3, c’est le résultat de 2 et encore 1). Idem pour « quatre » ; si les enfants ont compris les 3 premiers nombres (et il ne faut procéder à cet enseignement que quand c’est le cas), ils ont la possibilité d’accéder à la signification du mot « quatre » en généralisant celle de « un », de « deux » et de « trois » : si c’est le cas, ils apprennent d’emblée que 4, c’est 3 et encore 1.
Lorsqu’il procède ainsi, l’enseignant enseigne une forme de comptage très différente du comptage numérotage, parce que la correspondance terme à terme qu’il théâtralise n’est pas celle entre 1 mot et 1 objet mais la correspondance entre 1 mot et la pluralité des objets déjà pris en compte (ce n’est pas un comptage « à la Gelman »). Lorsqu’un enfant comprend cette forme de comptage, chaque mot prononcé désigne pour lui un vrai nombre puisqu’il désigne la nouvelle pluralité obtenue après l’ajout de 1 ; c’est la raison pour laquelle on peut alors parler de l’enseignement d’un « comptage dénombrement ». Il est sûr que l’on ne peut pas espérer enseigner avec succès le comptage dénombrement aussi précocement, ni aussi loin, qu’il est possible de le faire avec le comptage numérotage. Mais si l’on veut, plus tard, voir l’édifice prendre de la hauteur, il convient d’assurer de solides fondations.
Les enseignants peuvent aussi utiliser un « comptage dénombrement explicite ». Il y a deux façons de rendre un comptage dénombrement explicite. La première consiste à dire : « 1 et encore 1, 2 ; et encore 1, 3 ; et encore 1, 4 ». En effet, un comptage dénombrement est un comptage où l’on cherche à faire comprendre le calcul sous-jacent au dénombrement ; verbaliser ce calcul ne peut que favoriser cette compréhension. La seconde façon consiste, lors d’un comptage dénombrement, à exprimer le nombre total résultant de l’ajout successif des unités, en spécifiant la nature de cette unité : « un jeton, deux jetons, trois jetons… ». En effet, dans l’expression « trois jetons », la syntaxe de ce petit groupe nominal fait que le mot « trois » réfère à une pluralité, il n’est pas un numéro. Or, la signification des mots-nombres que le comptage dénombrement cherche à privilégier est celle de pluralités, celle que l’on appelle aussi la signification cardinale des mots-nombres.
De même que les points cardinaux (nord, sud…) sont ceux qui servent de repères pour s’orienter dans l’espace, la signification cardinale des mots-nombres est celle qui doit guider la pratique pédagogique des enseignants de maternelle. On remarquera d’ailleurs que dans les décompositions d’un nombre (trois, c’est deux et encore un, par exemple), chacun des mots-nombres prononcés a une signification cardinale. Faire le choix de privilégier les décompositions et le comptage dénombrement, c’est privilégier la signification cardinale des mots-nombres et, partant, c’est permettre un apprentissage explicite des nombres et du calcul.
Renouer avec la culture pédagogique des pays francophones
Faire le choix pédagogique de privilégier l’usage de décompositions des nombres et le comptage dénombrement, est-ce renouer avec la culture pédagogique de l’école maternelle française ? Nous allons voir que c’est effectivement le cas.
Dans un ouvrage publié dans les années 50 (Brachet, Canac et Delaunay, 1955), le premier de ces auteurs s’exprime ainsi : « Ce n’est pas, nous semble-t-il en remuant (l’auteur veut dire : en comptant numérotant) l’un après l’autre les quatre jetons d’une collection que l’enfant forme la notion de quatre et des décompositions. Ce serait plutôt, croyons-nous, en contemplant, à bonne distance, et d’une vue d’ensemble, simultanée, la constellation de 4 objets, que l’enfant sera illuminé par le nombre 4, qui est 2 + 2 et 3 + 1 ». Le mot « illumination » est évidemment malheureux mais le propos de ce pédagogue serait resté complètement d’actualité s’il avait dit : « Imaginer les différentes façons de dessiner les 4 points de la constellation du dé, est l’un des moyens par lequel l’enfant peut accéder au fait que 4, c’est 2 + 2 et c’est 3 + 1 ». L’important est évidemment que ce pédagogue se livrait à une critique du comptage (numérotage) et mettait la connaissance du nombre 4 du côté de la connaissance de ses décompositions.
De même, trouve-t-on un équivalent de la notion de comptage dénombrement dans les écrits des pédagogues anciens. C’est souvent à travers les propos des Inspectrices Générales des écoles maternelles que l’on sait aujourd’hui ce qu’était la culture pédagogique à l’époque. L’une d’elles, J. Bandet (1962), préconise cette forme d’enseignement du comptage, dans les cas où les unités ne sont pas déplaçables. Elle préconise d’utiliser un cache et de découvrir progressivement les unités :
Puis l’enseignant découvre un point de plus en disant : « quatre », etc. Pourquoi cet emploi d’un cache ? Cette pédagogue s’appuie sur un phénomène que les psychologues ont bien étudié : l’être humain a la possibilité de traiter jusqu’à 3 unités en parallèle, sans être obligé de focaliser son attention successivement sur chacune d’elles, phénomène que l’on appelle le « subitizing » (Fischer, 1991 ; Piazza & col, 2011). Lorsqu’on enseigne le comptage ainsi, on peut dire que, d’une certaine façon, l’enfant qui a compris les 3 premiers nombres voit « un », puis « deux » puis « trois » ; chacun de ces mots est mis en correspondance avec la pluralité que l’enfant « voit » et, lorsque l’enseignant fait apparaître l’unité suivante en disant : « quatre », l’enfant a la possibilité de généraliser la signification des mots « un », « deux » et « trois » en associant le mot « quatre » à la pluralité correspondante. Il s’agit bien d’une forme d’enseignement du comptage dénombrement.
Mais c’est encore Henri Canac qui renseigne le mieux sur ce qu’est la culture pédagogique de l’école française concernant les apprentissages numériques après 1945. Dans un texte publié d’abord dans une revue en 1947, puis dans un livre (Brachet & col, 1955) et enfin dans un ouvrage rédigé par une commission d’experts réunis par l’UNESCO autour de Gaston Mialaret (Mialaret, 1955), il se livre à une critique sévère du comptage (numérotage) : « …dans la plupart de nos classes enfantines ou préparatoires, il n’est pas sûr en dépit de quelques apparences spécieuses, qu’on s’élève beaucoup au-dessus du dénombrement mécanique. » (p. 12) Il n’utilise pas l’expression « comptage numérotage », bien sûr, il utilise même le mot dénombrement qui porte à confusion, mais comment ne pas voir les prémisses d’une analyse du comptage numérotage quand il dit ceci d’un enfant qui compte (numérote) : « dans l’incapacité où il se trouve d’opérer d’un seul coup, il se récite mentalement la suite des nombres, les noms ainsi proférés, surtout s’ils sont nettement scandés, constituant à leur manière des objets concrets » (p. 12). Et il professe du mépris pour ce comptage (numérotage), trop de mépris même, parce qu’il nie les quelques progrès qu’il permet : « Le maniement de bûchettes, la gesticulation digitale, le preste tracé de barres sur l’ardoise, peuvent à la rigueur développer la dextérité de la main ; mais cette précieuse qualité trouve de meilleures occasions de s’affirmer dans d’autres disciplines ».
Dans le même texte, Henri Canac met ensuite en avant la valeur cardinale des nombres et il présente une « méthode nouvelle » qui « forme à (son) sens, une des meilleures conquêtes de la pratique pédagogique au cours du dernier quart de siècle. » Cette méthode consiste à étudier les nombres dans l’ordre et elle conduit les enseignants : « à construire (définir, poser), le nouveau nombre par adjonction de l’unité au nombre précédent, puis à étudier ses diverses décompositions en nombres moins élevés que lui. »
Ainsi, avec cette méthode, il y a un moment pour l’étude du nombre 3, suivi d’un moment d’étude de 4, puis de 5… jusqu’à 10. Chaque nouveau nombre étudié est défini comme résultant de l’ajout de 1 au précédent. L’étude du nombre N commence donc par un comptage dénombrement jusqu’à N. Et, pour chaque nombre, on consacre beaucoup de temps à en étudier les décompositions. Il ne faut pas se méprendre : ce n’est pas une conception « behavioriste » des apprentissages qui guide ces pédagogues ; ils veulent avant tout choisir une méthode qui évite un premier écueil : le comptage (numérotage) 1 à 1, notamment sur les doigts. Canac en parle d’ailleurs comme d’une « gesticulation digitale ». L’objectif de ces pédagogue est de « bien débuter » les élèves.
Comment, selon Henri Canac, reconnaît-on un élève « mal débuté » ? Au fait qu’il ne mémorise pas les résultats d’additions élémentaires et qu’il compte jusque tard sur ses doigts : « Dans de nombreux cours élémentaires, ou même cours moyens, on trouve souvent de grands benêts qui comptent sur leurs doigts (en cachette lorsque M. l’Inspecteur est là) ou qui, sommés de résoudre une simple opération, comme 8 + 5, se récitent intérieurement à eux-mêmes : 8, 9, 10, 11, 12, 13 en évoquant des doigts imaginaires. » Henri Canac fait ainsi le lien entre l’enfermement dans le comptage 1 à 1 et l’absence de mémorisation des résultats d’addition.
En fait, le thème de la mémorisation des résultats d’additions est peu présent dans le texte d’Henri Canac. En revanche, il est omniprésent dans un texte antérieur, le Rapport de MM les Inspecteurs Généraux Marijon et Leconte sur les conférences pédagogiques de 1928 (Savard, 1940). C’est donc chez les pédagogues du « quart de siècle » d’avant 1945, ceux qui sont à l’origine de la conquête pédagogique que constitue la méthode d’étude de chaque nombre l’un après l’autre, qu’il faut aller chercher le complément d’information nécessaire.
Il semblerait que ces conférences pédagogiques de 1928 aient plutôt pris la forme d’ateliers dans lesquels les instituteurs devaient répondre à des questions du style : « Quelle doit être la part de la réflexion et de la mémoire dans l’enseignement des premières notions de calcul ? » « Convient-il d’apprendre par cœur la table d’addition? Vaudrait-il mieux exercer les élèves à combiner les nombres en utilisant les notion de compensation, de voisinage, de symétrie et de décomposition que leur intuition conçoit sans effort ? »
La réponse est sans ambages : « Ce n’est qu’après avoir bien réfléchi, comparé, raisonné même, qu’une notion est confiée à la mémoire. » « L’on passe toujours trop rapidement sur l’étude des premiers nombres, dans la hâte d’arriver aux opérations,… ces brillantes opérations qui font la joie de certains maîtres et d’à peu près tous les parents. »
« D’abord, l’étude de la première dizaine de nombres contient en germe bien des idées et nécessite bien des gradations : nommer ces nombres tout en les réalisant matériellement avec des objets, recommencer avec haricots, des billes… /… combiner les premiers nombres par addition et soustraction, n’employer la répétition, pourtant nécessaire, qu’après s’être assuré que toutes les combinaisons ont été « senties » de telle façon que le rôle de la mémoire reste subordonné et final, ensuite écrire ces nombres et enfin s’élever au nombre dit abstrait, le seul sur lequel on opère finalement, tout cela qui est aujourd’hui si bien fait à l’école maternelle peut aussi servir de méthode pour la suite au cours préparatoire et au cours élémentaire. Bien entendu, lorsque la toute première initiation a été à ce point détaillée, les enfants ne doivent plus compter sur les doigts. »
On voit s’élaborer dans ce passage, la méthode que, plus tard, Henri Canac qualifiera de « nouvelle ». Il faut prendre ce qualificatif au sérieux : Henri Canac dit lui-même qu’elle « n’est pas sans parenté avec les méthodes nouvelles d’apprentissage de la lecture » et sans doute pensait-il que promouvoir son usage était une façon de s’inscrire dans le mouvement de l’Education Nouvelle, si puissant au moment de la Libération. Le fait qu’une telle méthode risque d’instiller l’ennui par son aspect répétitif (leçon du 3, du 4…) et, donc, fonctionner à rebours des idées qui ont présidé à son élaboration, est une autre histoire.
Et concernant la mémorisation des résultats d’additions dont le résultat dépasse dix ? La recommandation est très claire : « Il convient, selon nous, d’arriver très vite à la formation, par voie purement mentale, de 8 + 7 = 15, au moyen de 8 + 2 = 10, 10 + 5 = 15, étant entendu que ces exercices auraient été précédés de nombreuses réalisations manuelles et visuelles. ». On notera que l’usage d’une telle stratégies n’est pas accessible à un élève qui ne s’est pas approprié la décomposition : 7 = 2 + 5. De façon générale, il n’y pas d’usage de stratégies de décomposition-recomposition possibles pour obtenir le résultat d’une addition dont le résultat dépasse dix sans une bonne connaissance des décompositions des dix premiers nombres.
On peut donc résumer ainsi ce qu’était, en 1970, la culture pédagogique des premiers apprentissages numériques à l’école :
1°) L’enseignement doit éviter deux écueils : le comptage mécanique 1 à 1 et un apprentissage par cœur précoce des résultats des additions élémentaires.
2°) Comment éviter ces deux écueils ? En permettant aux élèves de s’approprier les décompositions des 10 premiers nombres avant d’utiliser, pour les additions dont le résultat dépasse 10, des stratégies de décomposition-recomposition.
Ainsi, la méthode « nouvelle » qui s’élabore à partir de 1923, met l’accent sur une étude progressive des nombres et de leurs décompositions parce qu’elle est un moyen d’éviter les deux écueils précédents, et non pour adopter une progressivité de type « behavioriste ». Ces pédagogues anciens prônent un tel découpage de l’étude des nombres parce qu’ils visent une meilleure compréhension des nombres et parce qu’ils considèrent cette compréhension comme la condition d’une meilleure mémorisation. Cette conception de l’enseignement n’a rien à voir avec le découpage de ce qu’il faut enseigner en fragments élémentaires afin de favoriser des conditionnements successifs. Or, c’est souvent ainsi que la doxa moderniste l’analysera par la suite.
1970 : les fondamentaux de la culture pédagogique de l’école sont préservés
Les analystes de la réforme des mathématiques modernes de 1970, Michel Delord notamment, ont surtout insisté sur les changements survenus à cette époque. Deux phénomènes ont principalement attiré leur attention. Le premier est que l’usage des signes d’opérations a été retardé : après 1970, seul le signe « + » était enseigné au CP, les signes « x » et « – » l’étaient en milieu de CE1 et aucun symbolisme n’était utilisé pour la division avant le CE2. Le second est qu’après 1970, on n’écrivait plus de « nombres concrets » au CP, il n’était plus recommandé que l’enseignant écrive au tableau des égalités telles que : « 4 pommes + 3 pommes = 7 pommes ; il n’était pas plus recommandé que les élèves les écrivent sur leur cahier.
L’étude de la DEPP montre que ces changements ne se sont pas traduits par une dégradation des performances. Cela s’explique : l’arithmétique scolaire, surtout dans les petites classes, est souvent une arithmétique orale et, bien évidemment, on a continué dans les classes à résoudre des problèmes d’addition itérée de la même quantité, mais sans parler de multiplication ; on a continué à proposer des problèmes de partage ou de groupement, mais sans parler de division et l’on a continué à dire dans la classe que : « 4 pommes plus 3 pommes égalent 7 pommes », même si on écrivait seulement l’égalité sans les unités. Si ces deux changements étaient si importants, comment expliquer qu’au final, 17 ans après la réformes des mathématiques modernes de 1970, les enfants de CM2 calculaient toujours bien ?
Mais, entre l’avant et l’après 1970, il y eut aussi des continuités, et elles étaient bien plus importantes que les discontinuités, parce qu’elles concernaient ce qui était au cœur de la culture de l’école d’avant la réforme : le rejet du comptage (numérotage) 1 à 1 et l’enseignement des décompositions des nombres.
Première continuité : le rejet de l’enseignement du comptage numérotage. Plus qu’un rejet, même : sa disparition. D’une certaine manière, on pourrait dire que le rêve de Henri Canac, des époux Fareng, de J. Bandet… s’est réalisé avec la réforme des mathématiques modernes : enfin, il n’y eut plus de séquences conduisant les enfants à « remuer des jetons », à se livrer à une « gesticulation digitale », etc. L’enseignement du comptage numérotage disparut du seul fait que tout apprentissage numérique fut banni de l’école maternelle et du début du CP (on est durant la période piagétienne de l’école). On notera d’ailleurs que l’Inspectrice Générale qui exerçait lors de la transition entre les anciens et les nouveaux programmes était J. Bandet, celle qui préconisait la forme d’enseignement du comptage dénombrement qui consiste à démasquer successivement les unités de la collection que l’on veut dénombrer. A-t-elle pensé qu’il valait mieux que tout comptage disparaisse de l’école maternelle parce qu’elle désespérait que les enseignants abandonnent l’enseignement du comptage numérotage ? Toujours est-il que la solution adoptée fut effectivement la plus radicale que l’on puisse imaginer.
Il y eut, de même, continuité concernant l’enseignement des décompositions des nombres : après 1970, elles restent très fortement mises en avant au CP, mais de manière différente. Au milieu des années 70, pour comparer la taille de deux collections, les élèves de début de CP utilisaient systématiquement la correspondance terme à terme : soit ils rapprochaient physiquement les éléments des deux collections, soit ils les reliaient en traçant des traits. Et dans les Ecoles Normales (là où s’effectuait la formation des maîtres avant les IUFM), on préconisait très fortement une activité qui s’appelait les « boîtes nombres ». Celle-ci commençait vers le mois de novembre au CP et durait jusqu’au mois de janvier. Elle conduisait les élèves à placer dans une même boîte des collections qui peuvent être mises en correspondance terme à terme (par exemple, une collection de 7 cubes, une autre de 7 trombones…). Pour désigner la propriété commune à ces collections (le nombre, donc), les élèves étaient assez vite en difficulté : certains ne connaissaient ni le mot-nombre correspondant, ni son écriture chiffrée (rappelons que l’on n’apprenait plus du tout le comptage à l’école maternelle : ni le comptage numérotage, ni le comptage dénombrement !). Pour désigner le nombre, une première possibilité consistait à adopter un symbole arbitraire : une spirale par exemple. Mais l’enseignant mettait fortement en avant un autre moyen : si l’on découvrait qu’une collection de 7 cubes, par exemple, a été placée dans la boîte correspondante alors qu’elle est formée avec une collection de 4 cubes rouges et une autre de 3 bleus, on vérifiait qu’il est possible de retrouver cette décomposition avec les autres collections de la boîte et on écrivait « 4 + 3 » sur la boîte : la boite devenait celle des collections que l’on forme en réunissant une collection de 4 et une autre de 3. Il était donc possible de désigner le nombre correspondant à cette boîte par l’écriture « 4 + 3 » sans connaître le chiffre 7 ni même le mot « sept ».
On utilisait ainsi ce que l’on appelait une « écriture additive » du nombre. Dans un premier temps, une « écriture additive » d’un nombre pouvait être utilisée avant de savoir comment ce nombre s’écrit en chiffres, dans un second temps, les deux étaient reliés. Il suffit d’ouvrir un fichier de l’époque pour s’apercevoir qu’un temps important était consacré à travailler les « écritures additives » des nombres et, donc, les décompositions. Et quand on y regarde de près, il y avait là une situation tout à fait intéressante pour apprendre à « combiner les nombres en utilisant les notion de compensation, de voisinage, de symétrie et de décomposition » (Marijon et Leconte, 1928).
Cette activité a été élaborée par Guy Brousseau, le fondateur de la didactique des mathématiques en France ; elle est décrite dans ce que l’on peut considérer comme l’un de ses articles les plus importants (Brousseau, 1972). Les adaptations qui en ont été faites et que l’on trouve dans divers ouvrages, prenaient souvent certaines libertés avec la progression originelle, mais toutes reposaient sur l’hypothèse que les enfants n’avaient pas encore un comptage assuré et qu’il fallait profiter de ce moment pour mettre fortement en avant les décompositions des nombres. Il y eut, de ce point de vue, une totale continuité entre l’avant 1970 et la période ayant suivi. C’est plus tard, en 1986, que s’est située la rupture, c’est aussi à partir de cette date que les performances des enfants se sont brusquement et fortement dégradées.
Concernant l’élaboration de la culture pédagogique de l’école française, on vient d’insister sur la continuité entre 1923 et 1986. Il est probablement injuste de ne pas remonter plus loin dans le temps en évoquant Ferdinand Buisson qui, parlant de la méthode intuitive qu’il préconise, précise en 1887 qu’elle « a pour but de faire connaître les nombres : connaître un objet, ce n’est pas seulement savoir son nom, c’est l’avoir vu sous toutes ses formes, dans tous ses états, dans ses diverses relations avec les autres objets ; c’est pouvoir le comparer avec d’autres, le suivre dans ses transformations, le saisir et le mesurer, le composer et le décomposer à volonté. ».
De plus, il faudrait vraisemblablement avoir une vision plus internationale et parler de renouer avec la culture pédagogique des pays francophones. Lors de conférences en Wallonie, divers pédagogues m’ont dit partager l’analyse que je leur présentais du comptage numérotage, m’informant que, lorsque des pédagogues wallons abordaient cette question, ils parlaient souvent de « comptage unaire » plutôt que de comptage numérotage.
Rémi Brissiaud
Laboratoire Paragraphe – Université Paris 8
A suivre…
Voir aussi :