Le 9 avril, le Café Pédagogique publiait deux projets de notes de services ministérielles sur l’enseignement des mathématiques à l’école primaire. De manière surprenante, la partie traitant des apprentissages numériques en maternelle faisait un éloge appuyé de l’apprentissage mécanique du comptage-numérotage. Le ministre faisait ainsi table rase des changements majeurs qui, dans les programmes 2015, ont créé un espoir de refondation de la pédagogie du nombre à l’école. La publication de ces notes étant annoncée comme imminente, il a fallu parer au plus pressé et dénoncer prioritairement cette seule partie alors que bien d’autres auraient pu être critiquées. Dans une interview à France-info, Jean-Michel Blanquer a déclaré : « S’il y a des choses contestables dans ce que j’ai écrit, parlons-en ». Faisons-le, dans ce premier texte en analysant la version définitive de la note sur le calcul et les opérations. Dans un second texte, à venir, nous analyserons l’autre note, sur la résolution de problèmes arithmétiques.
Le nombre en maternelle
Dans la version définitive, la partie concernant les apprentissages numériques en maternelle a été très largement remaniée, elle n’entre plus aussi frontalement en contradiction avec le programme 2015. Elle ne brille cependant ni par sa cohérence, ni par la rigueur de sa rédaction. Comme dans la première version, par exemple, on y lit que « très tôt, l’enfant manifeste des compétences relatives aux quantités » alors que les compétences en question sont relatives à des ordres de grandeur (le mot exact, en anglais, est « magnitude ») : l’homme, comme toutes les espèces animales, distingue de manière innée un gros tas de nourriture d’un petit tas, par exemple (voir le Café Pédagogique du 12 avril).
Il ne faut pas galvauder l’usage du mot « quantité » quand on veut parler des quantités discontinues, celles qui fondent le nombre (la quantité de gâteaux dans un paquet, par exemple). On ne peut pas dire d’un enfant qu’il traite de ces quantités s’il ne met pas en œuvre une correspondance terme à terme. Cette correspondance apparait de manière évidente lorsque l’enfant compare une quantité de jetons rouges à une autre de bleus en appariant les uns aux autres, par exemple. Elle existe également lorsqu’il compte : il s’agit alors d’une correspondance avec les symboles que sont les noms de nombres. Or, l’usage d’une telle correspondance et la compréhension de la façon dont elle permet de comparer des quantités ne sont pas si précoces et dépend d’un choix pédagogique crucial : le pédagogue enseigne-t-il le comptage-numérotage ou le comptage dénombrement (rappelons que celui-ci théâtralise le calcul +1 répété sous-jacent au comptage) ?
La nouvelle version, comme l’ancienne, entretient la confusion entre une compétence innée, celle concernant les « magnitudes », et une conquête culturelle : l’accès à la comparaison des quantités, c’est-à-dire au nombre. Bref, cette nouvelle version du texte n’aidera guère un formateur qui voudrait faire comprendre aux professeurs les raisons des changements intervenus en 2015 et la meilleure façon de les mettre en œuvre.
« Le » sens des opérations
Cette expression est utilisée 5 fois dans ce court texte, elle y figure même en gras. Son usage est surprenant parce que, dans les écrits pédagogiques, classiquement, on parle « des » sens de la soustraction, par exemple, et non « du » sens de cette opération. Et la plupart des pédagogues s’accordent pour distinguer trois principaux sens à cette opération : la recherche d’un reste, celle d’un complément et, enfin, celle d’une différence (cas des situations de comparaison).
Le mode d’expression classique a l’avantage de rappeler que maitriser une opération permet de se comporter de la même manière (faire une soustraction, par exemple) dans des situations (reste, complément et différence) qui, a priori, n’ont pas grand-chose en commun. « La mathématique est l’art de donner le même nom à des choses différentes » écrivait avec raison Henri Poincaré. Choisir d’utiliser l’expression « le sens de la soustraction », c’est masquer cette caractéristique essentielle de cette opération. Il en est évidemment de même avec les autres opérations.
La critique précédente pourrait paraitre excessive parce que différents sens de la soustraction sont présentés dans l’autre note ministérielle, celle consacrée à la résolution de problèmes arithmétiques. Plus précisément, cette seconde note parle des « différents types de problèmes se résolvant par une même opération ». Or, il y en a pléthore (dans la catégorisation de Vergnaud, qui n’est pas exhaustive, il y en a plus de 10 !). Les principaux sens d’une opération et les différents types de problèmes se résolvant par une même opération sont donc deux notions différentes. Celle de « principaux sens d’une opération » n’apparait dans aucune des deux notes, affaiblissant le propos de l’une comme de l’autre. Nous verrons d’ailleurs, dans le texte à venir, que ce manque de rigueur conduit Jean-Michel Blanquer à faire des recommandations aventureuses concernant la résolution de problèmes arithmétiques.
Les deux techniques de soustractions posées
On lit dans la note consacrée au calcul que « Pour la soustraction, le choix de l’algorithme (compensation ou cassage de l’unité de numération supérieure) relève de l’équipe d’école. On aura intérêt à conserver le même durant les quatre années concernées (du CE1 au CM2). » Avec une telle consigne, une équipe d’école se trouve typiquement confrontée à une injonction contradictoire : elle n’a guère de chance de la respecter si elle veut favoriser la réussite chez les élèves. C’est ce que nous allons montrer.
Analysons chacune de ces deux techniques en prenant comme exemple le calcul de 475–128 (on notera qu’il y a une retenue au niveau des unités). La technique du « cassage de l’unité de numération supérieure » consiste à transformer 475, c’est-à-dire « 4 centaines, 7 dizaines et 5 unités », en « cassant » l’une des 7 dizaines et en la remplaçant par 10 unités. Ainsi, le grand nombre de la soustraction devient : « 4 centaines, 6 dizaines et 15 unités ». Dès lors, le retrait de « 1 centaine, 2 dizaines et 8 unités » ne pose plus problème parce que le calcul de la soustraction 15–8 fait partie des savoir-faire préalables.
L’autre technique, traditionnellement utilisée en France avant la réforme des mathématiques modernes de 1970, consiste à calculer une autre soustraction que celle qui est posée. Plutôt que de calculer 475–128, on calcule : « 4 centaines, 7 dizaines et 15 unités » (on est passé de 5 unités à 15 unités) moins « 1 centaine, 3 dizaines et 8 unités » (on est passé de 2 dizaines à 3 dizaines). Elle se justifie du fait que 475–128= (475+10) – (128+10). Comprendre cette seconde technique nécessite d’être convaincu que les deux soustractions conduisent au même résultat ! Or, il s’agit d’une propriété conceptuelle de haut niveau, totalement inaccessible à un grand nombre d’élèves de CE1. L’enseignant, dès lors, est obligé de conditionner ces élèves à l’usage d’une suite de règles par leur usage mécanique et répété. Ce n’est ni très formateur d’un point de vue intellectuel, ni très efficient parce qu’avec les élèves les plus faibles, un apprentissage basé sur un usage mécanique de règles est chronophage pour un résultat qui est loin d’être garanti.
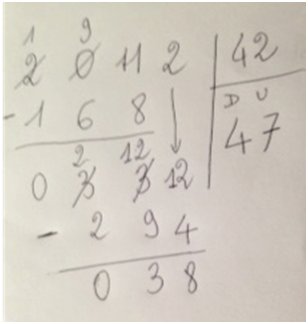
Mais alors, pourquoi ne pas choisir la première technique et la conserver ? Parce qu’en cas de « 0 intercalé » (cas de 1305–528, par exemple), on ne peut plus « casser une dizaine », il faut casser l’une des 3 centaine et la remplacer par 9 dizaines et 10 unités. Et ce cas n’est pas le plus complexe ! Imaginons celui où il y a deux ou trois 0 intercalés… Par ailleurs, quand les retenues sont trop nombreuses (retenue aux unités, aux dizaines…), cette technique conduit à des écritures où l’on distingue difficilement ce qui est barré de ce qui ne l’est pas. Comme la technique de la division nécessite de faire une suite de soustractions, la plupart des enseignants de CM2 préfèrent que leurs élèves utilisent la technique traditionnelle (la division de 2012 par 42 est exécutée ci-contre en exemple).
Les deux algorithmes ont donc des caractéristiques très différentes et le pédagogue semble enfermé dans un dilemme : choisir celui qui est facile à comprendre au CE1 mais qui rend l’apprentissage ultérieur de la division plus difficile ou bien choisir celui qu’un grand nombre d’élèves ne comprend pas au CE1. Quelle solution ? Il suffit d’enseigner la « technique » facile à comprendre au CE1 et l’autre à partir du CE2. Le mot « technique » a été mis entre guillemets dans le cas de l’algorithme par « cassage de la dizaine » parce qu’à strictement parler, il ne s’agit pas d’une « technique de soustraction » du fait qu’aucune propriété conceptuelle propre à cette opération n’y est utilisée. Il s’agit d’une tache de réinvestissement des connaissances en numération décimale (quels liens entre les centaines, dizaines et unités d’un nombre ?) qui, de plus, permet aux élèves les plus faibles de continuer à construire ces connaissances. Au CE2, en revanche, les élèves sont plus âgés et la propriété conceptuelle qui fonde la technique traditionnelle devient accessible à la quasi-totalité des élèves.
L’objection consistant à dire que, pour viser l’automatisation, il conviendrait de garder la même « technique », le changement faisant obstacle à cette automatisation, repose sur une mauvaise interprétation de ce que nous venons d’expliciter. En effet, les enseignants qui font le choix de changer de « technique » ne visent pas l’automatisation au CE1. Ils visent à consolider une compétence essentielle dont toutes les évaluations montrent qu’elle fait défaut chez de trop nombreux élèves : comprendre l’écriture des nombres à plusieurs chiffres.
Ce choix est celui que font, aujourd’hui, des milliers de professeurs des écoles. Leurs élèves, en CE2, acceptent volontiers l’idée de changer de technique parce que l’enseignant le justifie en expliquant que la nouvelle leur permettra de calculer des soustractions plus complexes. Quelle est l’argumentation du ministre pour affirmer que le choix qu’il préconise (« On aura intérêt à conserver le même [algorithme] durant les quatre années concernées. ») serait meilleur ? Comme il le suggérait dans son interview sur France Info, certains de ses choix sont contestables.
Mémoriser les résultats d’additions et de multiplications élémentaires
En lisant la partie de la note consacrée à ce thème, on est tout d’abord étonné du fait que la mémorisation des résultats d’additions et de multiplications élémentaires y soient traités à l’identique : « Chaque résultat est d’abord exploré et construit en classe, récité et réinvesti, noté dans le cahier de référence en mathématiques. Dans un deuxième temps seulement un travail à la maison peut être demandé. » Or, les recherches en psychologie cognitive ont mis en évidence que les résultats de multiplications élémentaires ne se mémorisent pas comme ceux de l’addition. Les travaux qui font référence sur le sujet sont ceux de Jean-Paul Fischer.
La mémoire des résultats de multiplications repose plus sur de l’association verbale que ceux de l’addition. En psychologie, la mémorisation des résultats de multiplications est caractérisée par sa forme « déclarative ». En pédagogie, on dirait plus banalement : « connus par cœur ». Ainsi, imaginons une petite expérience consistant à interroger quelqu’un par surprise : « quatre fois huit ? ». La réponse « trente-deux » jaillit le plus souvent. Chez la personne qui a bien mémorisé le répertoire multiplicatif, l’association verbale entre « quatre fois huit » et « trente-deux » est forte et les termes de la multiplication appellent de façon irrépressible le résultat. C’est moins le cas si la question est : « huit plus quatre ? ». Bien sûr qu’il y a de l’association verbale entre cette expression et la réponse, « douze », mais elle moins forte et ce résultat ne s’obtient pas en mémoire sans la mise en œuvre, à notre insu, d’une procédure du type 8+2+2, par exemple. Dans le cas de l’addition, on dit que le résultat est mémorisé sous forme procédurale et que la procédure correspondante est automatisée. C’est parce qu’elle est automatisée que l’on n’a pas conscience de la mise en œuvre d’une telle procédure. En résumé : la mémorisation des résultats d’opérations élémentaires fait appel à deux processus distincts : à la mémorisation déclarative dans le cas de la multiplication, à l’automatisation d’une procédure dans celui de l’addition.
Quel éclairage cette distinction jette-t-elle sur les pratiques scolaires ? Concernant les additions élémentaires, il est très important, dès le CP, de favoriser l’usage de stratégies de décomposition-recomposition pour en favoriser l’automatisation : 8+6=8+2+4, 9+7=9+1+6, etc. De manière étonnante, aucune allusion n’y est faite dans la partie de la note ministérielle dédiée à la mémorisation des faits numériques. En revanche, le ministre y parle constamment de « tables d’additions » comme si cet outil jouait un rôle déterminant dans la mémorisation des résultats, ce dont on peut fortement douter. Jamais les « tables d’additions » n’ont eu un rôle équivalent aux « tables de multiplications » dans l’école française. C’est pour de bonnes raisons !
Et concernant la multiplication ? Le ministre écrit : « le résultat du produit 6×8 étant à apprendre, le maître demande d’abord à tous les élèves de chercher plusieurs façons de calculer 6×8 (6×4+6×4=24+24=48 ; 6+6+6+6+6+6+6+6=12, 18, 24…48 ; 8+8+8+8+8+8=16+16+16=32+16=48 ; 6×8=5×8+1×8 ; etc.), puis note au tableau toutes les procédures trouvées par les élèves, puis fait noter dans le cahier de référence le résultat et quelques procédures significatives, puis propose quelques calculs en ligne ou posés comme 616×8 ou 816×66, enfin demande aux élèves d’apprendre la table de 8 jusqu’à 6×8 sachant que les résultats 2×8, 3×8,4×8 et 5×8 ont déjà été travaillés. »
Là encore, la démarche préconisée par le ministre est fortement critiquable : telle qu’elle est décrite, on a l’impression qu’un élève confronté à l’interrogation « 6 fois 8 ? » devrait passer en revue les différentes façons d’obtenir le résultat avant de choisir celle qui lui convient le mieux. Ce n’est certainement pas en s’y prenant ainsi qu’on favorisera l’association verbale entre « six fois huit » et « quarante-huit ». Le seul fait de réfléchir à la façon dont je vais calculer empêche l’association verbale. De nombreuses situations pédagogiques, dont le jeux « Le compte est bon », permettent de chercher les différentes stratégies permettant d’obtenir un nombre donné. Ces situations sont très intéressantes mais elles ne visent pas prioritairement la mémorisation du répertoire multiplicatif.
Pour que l’association verbale nécessaire s’installe, il faut que l’enfant privilégie une stratégie, toujours la même. Mais laquelle ? Depuis longtemps, de très nombreux enseignants répondent : celle qui consiste à chercher mentalement la réponse dans la table. Mais qu’est-ce que « la » table de multiplication par 3, par exemple ? C’est celle qui commence par « 3 fois… » (il suffit de regarder au dos des cahiers de brouillon !) : « 3 fois 1, 3 » ; « 3 fois 2, 6 » ; « 3 fois 3, 9 » ; « 3 fois 4, 12 »…
En sciences cognitives, cette préférence pour ce type de table (plutôt que « 1 fois 3 » ; « 2 fois 3 » ; « 3 fois 3 »…) s’explique aisément. Quand un acteur a oublié son texte, il suffit de lui rappeler les premiers mots pour qu’il se remémore la suite. Cela s’explique du fait que le début d’une expression verbale fonctionne comme « indice de rappel » de la suite. Dans le contexte d’une table de multiplication, à terme, dès que l’enfant entendra « 3 fois… », les résultats possibles seront préactivés dans son cerveau (3, 6, 9, 12…), ce qui l’aidera à retrouver le bon résultat (il n’aura pas à chercher dans toute sa mémoire des nombres).
Pratiquement, l’enseignant commence par construire la table avec les élèves et, surtout, par leur faire découvrir que les résultats vont de 3 en 3, ce qui constitue la clé pour savoir la réciter. Le jeu du furet aide les enfants à mémoriser la suite des faits numériques : un premier enfant dit « 3 fois 1, 3 », le suivant « « 3 fois 2, 6 » et ceci jusqu’à « 3 fois 10, 30 », puis on continue en reculant sur la table. On remarquera que chaque enfant prononce le fait numérique en entier et non le résultat seulement : on vise l’association verbale et seule l’expression complète du fait numérique la consolide.
Il faut ensuite aider les élèves à retrouver les résultats de la fin de table car ils sont les plus difficile à mémoriser. Et ceci, sans avoir besoin de réciter la table depuis le début. Dans ce but, on peut leur apprendre à s’appuyer sur deux résultats faciles : « 3 fois 5, 15 » et « 3 fois 10, 30 ». Faisons-le pour calculer 3 fois 6 et 3 fois 9, par exemple. On ne calcule évidemment ni 6+6+6, ni 9+9+9 parce qu’au CE1 c’est difficile et parce que ce serait s’« échapper » de la table, basée sur la récitation de 3 en 3. On raisonne ainsi : dans la table, « 3 fois 6 », c’est juste après « 3 fois 5, 15 », c’est donc 15+3, 18. De même, « 3 fois 9 », c’est juste avant « 3 fois 10, 30 », c’est donc 30–3, 27. L’élève échappe à la récitation depuis le début ! Afin qu’il puisse s’interroger lui-même, on peut lui fournir une table vide, sans les résultats, sauf peut-être ceux de 3 fois 5 et 3 fois 10 qui sont les points d’appui.
La proposition pédagogique qui vient d’être faite est très différente de celle du ministre : bien distinguer les séquences visant à mémoriser les résultats et celles visant à explorer une pluralité de stratégies (ce qui correspond à un style d’enseignement plus explicite), faire analyser d’emblée la structure d’une table aux élèves (les résultats vont de n en n) plutôt que d’étudier les différents résultats dans différentes séances, privilégier une seule façon de dire la table de 3 (3 fois…), celle dont tout conduit à penser qu’elle favorise le mieux la mémorisation…
Quels arguments en faveur d’une telle démarche ? Elle est une adaptation de celle qui fut privilégiée pendant des dizaines d’années dans l’école française, elle a donc une validité écologique bien établie. Elle est même une modernisation de cette démarche avec l’apport du jeu du Furet, de la table incomplète… Et, surtout, grâce aux travaux en sciences cognitives, il est possible aujourd’hui d’expliquer aux enseignants français pourquoi c’est vraisemblablement l’une des plus efficientes : on se réfèrera, par exemple, à la notion d’indice de rappel et au fait que le passage d’une logique verbale (celle de la récitation de la table) à une logique spatiale (chercher où est tel ou tel résultat dans la table) aide à la construction de connaissances déclaratives. L’un des principaux résultats en neurosciences cognitives, résultat qui a d’ailleurs valu un prix Nobel aux chercheurs l’ayant établi, est que la spatialisation joue un rôle crucial dans la mémorisation.
Le ministre a-t-il de tels arguments ? Dans l’interview donnée à France Info, il dit préconiser ce qu’il y a de meilleur pour le progrès des élèves. Sur un thème comme celui-ci, qu’est-ce qui lui donne autant d’assurance ? Il affirme s’être appuyé sur la recherche. Laquelle ? Y a-t-il un seul chercheur prêt à défendre l’idée de la supériorité de ses propositions par rapport à d’autres telles que celles exposées ici ?
3 axes d’analyse de la note du ministre : aucun ne la sauve
Avec les nouveaux programmes, depuis 2015, l’Education nationale recommande d’enseigner les nombres à l’école maternelle et au cycle 2 en accordant la priorité au calcul. Aujourd’hui, l’une des principales théoriciennes du domaine, Elisabeth Spelke, professeur à Harvard et nouvelle membre du Conseil scientifique de l’Éducation nationale, déclare : « [I reject] the thesis that counting is central to number » ? En 1990, Josette Fargeas, inspectrice générale, écrivait dans l’ouvrage théorique connu sous le nom de Ermel Grande Section : « s’agissant des jeunes enfants, l’hypothèse est posée que dans la genèse du concept de nombre, le nombre pour compter joue le premier rôle et le plus important ». On ne peut évidemment pas enseigner les nombres de la même manière en 2018 qu’en 1990 ! Nous vivons donc une sorte de révolution dont l’enjeu est l’accès au calcul : celui-ci doit-il être favorisé d’emblée ou bien les élèves doivent-ils faire un long détour par l’usage du comptage-numérotage ? Le large débat qui a précédé les programmes 2015 s’est conclu par le choix d’accorder la priorité au calcul, dans l’espoir d’améliorer les médiocres résultats des écoliers français.
Un premier axe d’analyse de la note ministérielle est donc le suivant : dans quelle mesure cette note accompagne-t-elle cette révolution ? De ce point de vue, la première mouture du texte était une véritable catastrophe, confortant les pratiques ayant dégradé les performances des écoliers français. La version définitive accompagne très mal la révolution nécessaire et elle le fait, semble-t-il, à contrecœur. C’est ainsi que sur le site Eduscol, dans une bande dessinée censée résumer le propos de la note pour la maternelle, les deux préconisations retenues sont : « Apprendre à compter grâce à des comptines, etc. » et « Découvrir les nombres écrits : tracé des chiffres, dates sur le calendrier, etc. ». Cela aurait pu être : « Comprendre le calcul +1 répété qui explique le comptage » et « Dans des situations concrètes et pour chacun des premiers nombres, l’exprimer en nombres plus petits que lui ». Le ministre est très clairement dans l’ignorance de ce qui se joue actuellement dans les classes maternelles.
Un autre axe d’analyse concerne des choix pédagogiques ou didactiques d’un autre niveau : quelle(s) technique(s) de la soustraction posée faut-il enseigner ? Comment favoriser la mémorisation des faits numériques ? De façon générale, ces questions doivent être considérées comme complexes et les réponses qui y sont apportées comme mal assurées. On ne peut que se rapporter aux pratiques de nos prédécesseurs, profiter de tous les éclairages possibles offerts par les sciences cognitives et la didactique et ne pas hésiter à innover en tenant compte de toutes les connaissances disponibles. Le ministre, lui, est très assuré dans ses réponses alors que celles-ci, comme nous l’avons montré ici, vont à l’encontre d’autres réponses pourtant bien étayées, notamment par les connaissances robustes en sciences cognitives.
Enfin, un dernier axe d’analyse concerne des préconisations d’un tout autre ordre encore, celui des conseils de gestion de la classe. Dans la seconde note, par exemple, on lit : « Lors des temps de recherche individuelle ou par groupe, l’enseignant doit veiller à circuler dans les rangs pour consulter les productions de chacun des élèves afin de pouvoir : – encourager leur mise en recherche ; – relancer le travail des élèves bloqués… ». Et, plus loin : « (si) aucun élève ne fait ce qui est attendu, l’enseignant ne doit pas renoncer à ce modèle ou attendre qu’il émerge nécessairement d’un élève de la classe. Il peut le proposer lui-même, par exemple en le présentant comme une méthode utilisée par un élève l’année précédente ».
Ces conseils n’ont rien de spécifiques aux mathématiques, ils relèvent de la pédagogie générale. Après la publication des notes ministérielles, de nombreux professeurs des écoles ont largement manifesté leur énervement sur les réseaux sociaux. La présence de ce type de conseils l’explique en grande part. Ils sont totalement inappropriés à un tel texte. Les professeurs des écoles se considèrent rarement comme des didacticiens des mathématiques mais ils se revendiquent, avec raison, pédagogues. Or, ils sont face à un ministre qui vient leur faire la leçon en énonçant des évidences concernant ce qui est au cœur de leur compétence professionnelle. Les professeurs des écoles mieux informés en didactique des mathématiques seront vraisemblablement plus énervés encore face à un ministre qui leur fait des leçons de pédagogie générale alors qu’à la lecture de son texte, il se révèle être un didacticien trop sûr de lui et peu informé des avancées en sciences cognitives.
Rémi Brissiaud
Professeur de mathématiques honoraire
Maitre de Conférences honoraire de psychologie cognitive
Chercheur associé au Laboratoire Paragraphe, EA 349 (Université Paris 8)
Membre du conseil scientifique de l’AGEEM
Directeur de la collection « J’apprends les maths avec Picbille » chez Retz
Sur les instructions Blanquer : le dossier
Bibliographie
Brissiaud R. (1994). Penser l’usage du mot « fois » et l’interaction oral / écrit lors de l’apprentissage initial de la multiplication. In Artigue M., Gras R., Laborde C, Tavignot P. (Eds) : Vingt ans de didactique des mathématiques en France (pp.195-202). Grenoble : La pensée sauvage.
Ermel (1990) Apprentissages numériques, cycle des apprentissages, grande section de maternelle, Paris : Hatier.
Fischer, J.-P. (1992). Apprentissages numériques: la distinction procédural/déclaratif Nancy: Presses
universitaires de Nancy.
Spelke E. (2017) Core Knowledge, Language, and Number. Language Learning and Development, 13- Issue 2: The Representation of Number: Origins and Development
